Show that for very large numbers the Stirling’s approximation gives n! ≅ √2πn nne−n
n! = nn − 1n − 2... 432Take the natural logarithm of n!
Related Solutions
Energy associated with nth orbit of H-atom is given by the expression, . Show that E_((n+l))-E_(n)=(13.6xx2)/(n^(3))eV~, when 'n' in very large.
View SolutionIf n is a natural number then show that n! + (n+1)! = (n+2)n!
View Solutionएक प्रतिउदाहरण देकर, दर्शाइए कि निम्नलिखित कथन असत्य है :
'यदि n एक विषम संख्या है, तो n एक अभाज्य संख्या है।'
View SolutionShow that the percentage error in the nth root of a number is approximately times the percentage error in the number.
View SolutionUsing Bohr's theory show that when n is very large the frequency of radiation emitted by hydrogen atom due to transition of electrom from n to is equal to frequency of revolution of electron in its orbit.
View SolutionState whether True or False:
If n is very large and p is very small then X follows Poisson distribution with n = m p.
View SolutionLet , where [x] and {x} are integral and fractional parts of x and . Then is equal to
View SolutionEnergy associated with the n-th orbit of H-atom is given by the expresion, E_(n)=(-13.6)/(n^2)eV . Show that E_((n+1))-E_(n)=(13.6xx2)/(n^(3))eV , when 'n' is very large.
View SolutionWhen n is very large and p is very small in the binomial distribution, then X follows the Poisson distribution with parameter m =
View SolutionIn Binomial distribution if n is very large and probability of success of p is very small such that np = m (constant) then...............distribution is applied
View SolutionIn Binomail distribution if n is very large and probability success of p is very small such that np = m (constant) then ............... distribution is appplied.
View SolutionIf the number of elements of set A are n, then show that the number of sub sets of A are .
View SolutionBy giving an example, show that the following is false:
"If n is an odd integer,then n is prime".
View Solution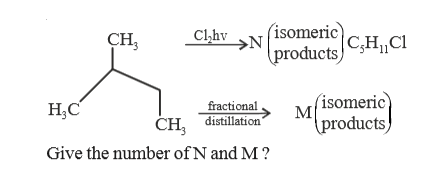
Give the number of N and M ?
View Solution
Give the number of N and M ?
View Solution
Give the number of N and M ?
View Solution
Give the number of N and M ?
View SolutionThe numerical value of N/n (where N is the number of molecules in a give sample of gas and n is the number of moles of gas) is
View SolutionIf n is a large whole number, then n^(2) (n^(2) - 1) will always split
View SolutionShow that for all natural numbers n.
View Solution