A random variable X has exponential distribution with probability density function fx = µe-µx x µ > 0The coefficient of variation of X isa 1/µb 1c µd √2
Correct option: b 1Explanation: The mean and variance of the exponential distribution are 1/µ and 1/µ2 respectively.Coefficient of Variation
Related Solutions
A random variable X has the following probability distribution:

View SolutionA random variable X has the probability distribution

View SolutionA random variable X has the following probability distribution:

then Var(X)=____
View SolutionA random variable X has the following probability distribution:

Then E(X) = …….
View SolutionA random variable X has the following probability distribution
Determine P(X<3)

View SolutionA random variable X has the following probability distribution find mean of x:
View SolutionA random variable X has the following probability distribution:
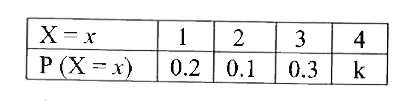
Then, the variance of X=
View SolutionA random variable X has the following probability distribution.
Then, the mean of X is

View SolutionA random variable X has the following probability distribution :

Then, the expected value of X is
View SolutionA random variable X has the following probability distribution :

View SolutionA random variable X has the following probability distribution:

Then, the variance of X is
View SolutionIf X is the random variable with distribution function F(x) given by,
the probability density function f(x)
View SolutionA random variable X has the following probability distribution

Then the variance of this distribution is
View SolutionThe probability distribution of a random variable X is
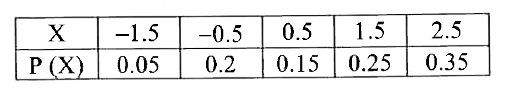
Then the c.d.f. Of X is
View SolutionA random variable X has the following probability distribution:

Find the expectation of the random variable X.
View SolutionThe distribution function F(x) of a random variable X is ……….
View Solutionयदि यादृच्छिक चर X के संगत प्रायिकता बंटन द्विपद बंटन है। किस यादृच्छिक चर के संगत न्यूनतम और अधिकतम प्रायिकता है।
View SolutionA random variable X has the following probability distribution: [[X=x,0,1,2,3], [P(X=x),(1)/(8),(1)/(2),(1)/(4),k]]
View SolutionConsider the probability distribution of a random variable X: Compute V(X/2)
View SolutionConsider the probability distribution of a random variable X.

View Solution