Consider the hydrogen molecule H2 as a rigid rotor with distance of separation of H-atoms r = 1.0Å. Compute the energy of J = 2 rotational level.
= 0.264 × 10−10 MeV = 2.64 × 10−5 eV
Related Solutions
In the potential energy curve for the formation of H2 molecule as a function of internuclear distance of H atoms, what happens at the minimum in the curve?
View Solution27 °C તાપમાને 200 g ઓક્સિજનની ઉષ્મીય ગતિ સાથે સંકળાયેલી ઊર્જા ........ J થાય.(ઓક્સિજનના અણુને rigid rotator ગણો.)
View SolutionThe energy of the electrons of a hydrogen atom at ground level is - 2.18 × 10 ^ (- 18) J. Determine the ionization energy of the hydrogen atom J mol ^ (- 1) unit.
View Solutionहाइड्रोजन परमाणु की निम्न ऊर्जा स्तर में ऊर्जा है | हाइड्रोजन परमाणु में क्वाण्टम संख्या = 2 के संगत स्तर की ऊर्जा होगी
View SolutionThe value of energy for the oxygen molecule (rotational rigid) will be
View SolutionFind the angular velocity of rotation of a hydrogen molecule on the first excited rotational level, if the distance between the centres of its atoms is 0.74 Å.
View SolutionEnergy Level Of Hydrogen Atoms
View Solutionএকটি হাইড্রোজেন পরমাণু কে আয়নে পরিণত করতে 13.6eV শক্তির প্রয়োজন হয়। এই পরমাণুর n=2 শক্তি স্তর থেকে ইলেকট্রনকে বিচ্ছিন্ন করতে কত শক্তির প্রয়োজন হবে?
View SolutionIf the electron in a hydrogen atom were in the energy level with n 3, how much energy in joule would be required to ionise the atom ? ( Ionisation energy of H - atoms is 2.18 xx 10^(-18) J ) :
View SolutionWhat is the energy level diagram for an atom? Calculate the energies of the various energy levels of a hydrogen atom and draw an energy level diagram.
View SolutionRotational energy levels of diatomic molecules are well described by the formula E_(J)=BJ(J+1) , where J is the rotational quantum number of the molecule and B its rotational constant. B is related to the reduced mass mu and the bond length R of the molecule through the equation B=h^(2)/(8pi^(2)muR^(2)) . In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule (hv=DeltaE) . The observed rotational transitions occur between adjacent rotational levels, hence DeltaE=E_(J+1)-E_(J)=2B(J+1) . Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation h(Deltaupsilon)=2B . By inspecting the spectrum provided, determine the following quantities for ^(2) C ^(p)C with appropriate units (a) Deltaupsilon (b) B (c) R
View SolutionRotational energy levels of diatomic molecules are well described by the formula , where is the rotational quantum number of the molecule and its rotational constant. is related to the reduced
mass and the bond length of the molecule through the equation .
In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule . The observed rotational transitions occur between adjacent rotational levels, hence . Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation .
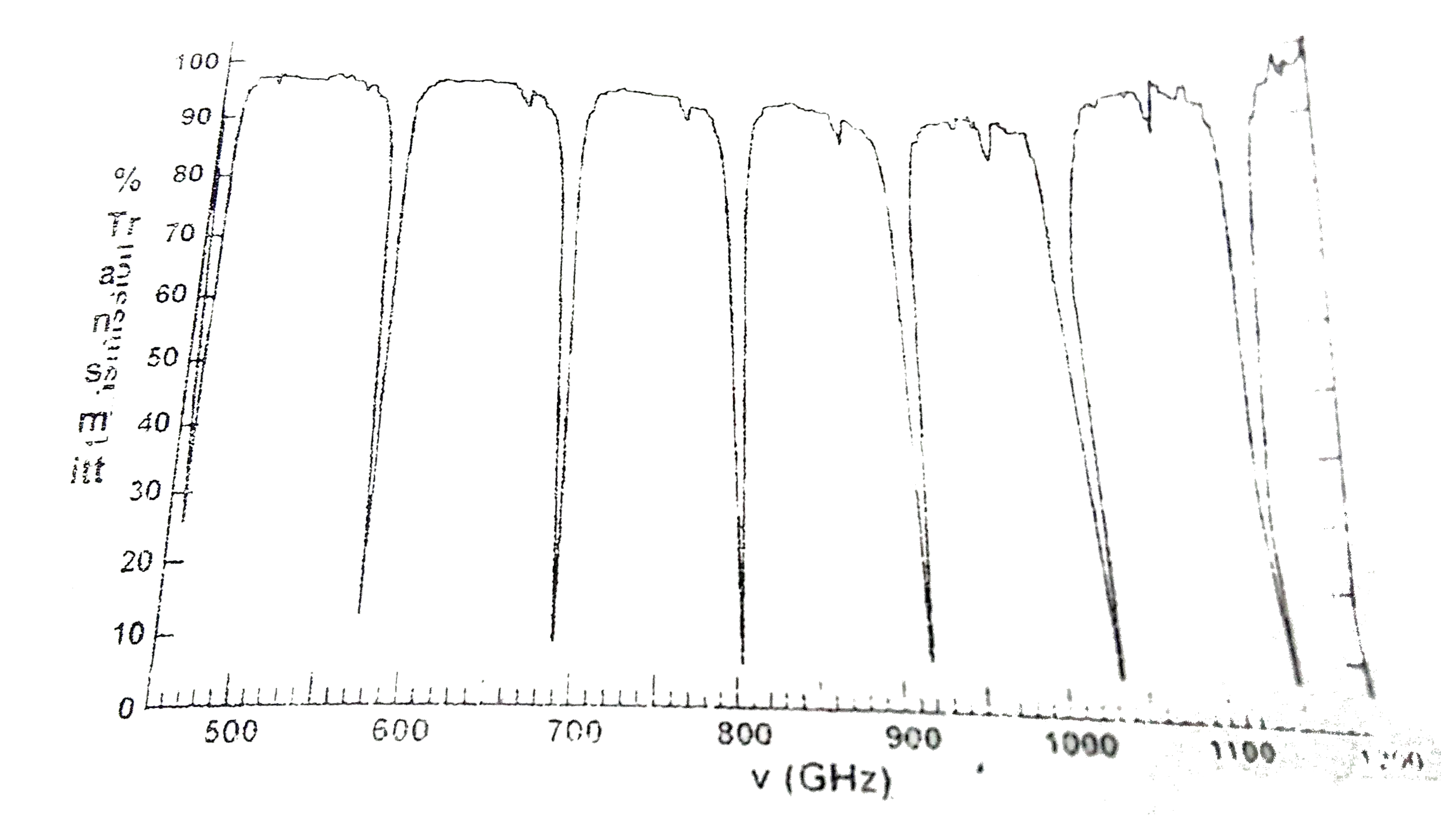
By inspecting the spectrum provided, determine the following quantities for with appropriate units
(a) (b) (c)
View Solutionहाइड्रोजन परमाणु की निम्न ऊर्जा स्तर में ऊर्जा -13.6 इलेक्ट्रॉन वोल्ट है। हाइड्रोजन परमाणु में क्वाण्टम संख्या =2 के संगत स्तर की ऊर्जा होगी
View SolutionIt is found experimentally that energy is required to separated a hydrogen atom into a proton and an electron. Compute the orbital radius and velocity of electron in a hydrogen atom.
View SolutionIt is found expertimentally that 13.6eV energy is required to separated a hydrogen atom into a proton and an electron. Compute the orbital radius and velocity of electron in a hydrogen atom.
View Solutionis found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.
View Solutionis found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.
View Solutionis found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.
View SolutionIt is found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron . Compute the orbital radius and the velocity of the electron in a hydrogen atom.
View SolutionIt is found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron . Compute the orbital radius and the velocity of the electron in a hydrogen atom.
View Solution