Simplify the Boolean expression A + B + CD + E’ + A + B + CD + E and choose the best answer.a A + B + Cb D + Ec A’B’C’d D’E’e None of these
A+B+CD+E + A+B+CD+E= A+B+CD+E+D+E’ Distributive Law= A+B+C.1 X+X’=1= A+B+CSo simplification of the Boolean expression A + B + CD + E’ + A + B + CD + E yields A+B+C
Related Solutions
सरल कीजिए :
(a + b) (c-d) + (a - b) (c + d) + 2 (ac + bd)
View Solutionसरल कीजिये
(a+b) (c-d) + (a - b)(c + d) +2 (ac + bd)
View SolutionIn figure, If LM || CB and LN || CD, prove that .
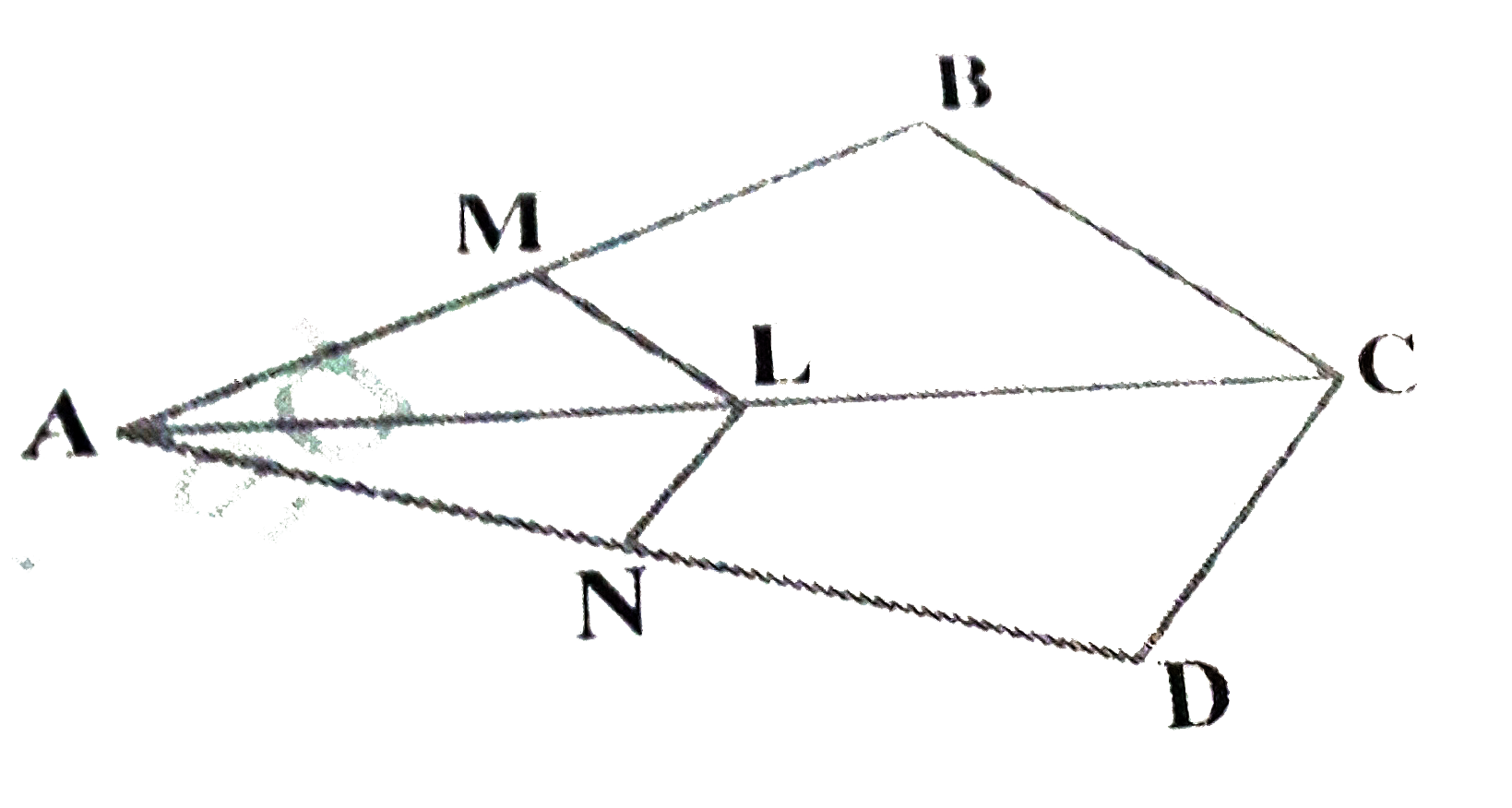
View SolutionIn figure, If LM || CB and LN || CD, prove that .

View SolutionIn this figure AB and CD intersect each other at E in such a way that DE=BE And EA=EC Prove that AD=CB
View SolutionThe determinant for
View SolutionThe determinant for
View SolutionThe determinant for
View SolutionIf A = ____. a) b)c) d)None of these
View SolutionIf A, B, C, D and E are points in a plane such that line CD bisects and line CB bisects right angle , then =
View SolutionIf A,B and C are the elements of Boolean algebra, simplify the expression (A'+B') (A+C')+B' (B+C). Draw the simplified circuit.
View SolutionProve the following Boolean relations:
View SolutionIf a,b,c and d are complex numbers, then the determinant Delta=|(2,a+b+c+d,ab+cd),(a+b+c+d,2(a+b)(c+d),ab(c+d)+cd(a+b)),(ab+cd,ab(c+d)+cd(a+b),2abcd)| is independent of
View SolutionIf are in proportion, then (a) (b) (d) None of these
View SolutionIf a,b,c,d,e are in continued proportion,then prove that (ab+bc+cd+de)^(2)=(a^(2)+b^(2)+c^(2)+d^(2))(b^(2)+c^(2)+d^(2)+e^(2))
View SolutionIf are in H.P., then are in (A) A.P. (B) G.P. (C) H.P. (D) none of these
View SolutionIf are in H.P., then are in (A) A.P. (B) G.P. (C) H.P. (D) none of these
View SolutionIf a, b, c and d are complex numbers then the determinant Delta=|(2,a+b+c+d,ab+cd),(a+b+c+d,2(a+b)(c+d),ab(c+d)+cd(a+b)),(ab+cd,ab(c+d)+cd(a+d),2abcd)|
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that .
View SolutionIn figure, ABCD is a parallelogram. A perpendicular BE is drawn from B to CD which meets CD at E. Prove that ABED will be a trapezoid.
View Solution