For the situation shown in figure below BP - AP = λ/3 and D >> d. The slits are of equal widths having intensity I0. The intensity at P would bea 4I0 b 2I0 c 3I0 d 7/2I0
Correct option cExplanation:
Related Solutions
For the situation depicted in the following figure, BP - AP = lambda // 3 and D » d. The slits are of equal widths, having intensity I_(0) . If the intensity of Pis kI_(0) , find k.
View SolutionIn a Young's double slit experiment with light of wavelength lamda the separation of slits is d and distance of screen is D such that D gt gt d gt gt lamda . If the fringe width is bea , the distance from point of maximum intensity to the point where intensity falls to half of maximum intensity on either side is
View SolutionIn a Young's double slit experiment with light of wavelength lamda the separation of slits is d and distance of screen is D such that D gt gt d gt gt lamda . If the fringe width is bea , the distance from point of maximum intensity to the point where intensity falls to half of maximum intensity on either side is
View SolutionIn a Young's double slit experiment with light of wavelength the separation of slits is d and distance of screen is D such that . If the fringe width is , the distance from point of maximum intensity to the point where intensity falls to half of maximum intensity on either side is
View SolutionThree narrow slits A, B and C are illuminated by a parallel beam of light of wavelength , P is a point on the screen exactly in front of point A. Slit plane is at a distance D from the screen. It is know that
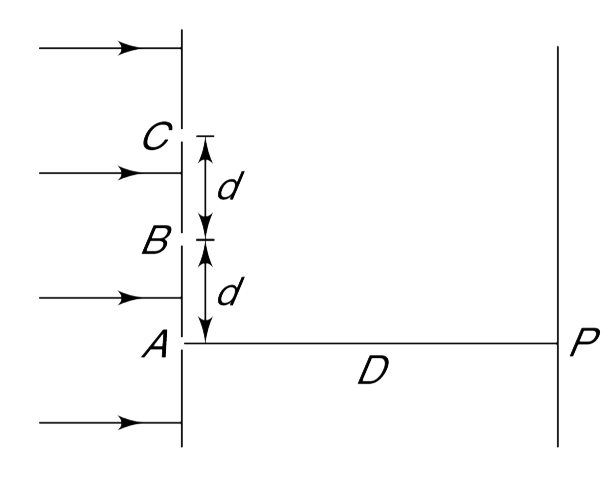
(a) Find d in terms of D and
(b) Write the phase difference between waves reaching at P from C and A.
(c) If intensity of P due to any of the three slits individu- ally is , find the resultant intensity at P.
View Solutionएक double slit के प्रयोग में स्लिटों के केंद्रों के बीच की दुरी d है और प्रत्येक स्लिट की चौड़ाई है। इसमें प्रयुक्त प्रकाश का तरंगदैर्घ्य है। केंद्रीय फ्रिंज की अधिकतम तीव्रता है। पहली दीप्त फ्रिंज की तीव्रता निकालें।
View Solutionयंग के द्विस्लिट प्रयोग में (d = स्लिटों के बीच की दूरी, D = स्लिटों से पर्दे की दूरी ) पर्दे के बिन्दु P पुर परिणामी तीव्रता, एक स्लिट के कारण तीव्रता के बराबर है। तब केन्द्रीय उच्चि्ठ से बिन्दु P की दूरी है
View SolutionIn Young's double-slit experiment (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit . Then, the distance of point P from the central maximum is
View SolutionIn Young's double slit experiment, (d=distance between slits, D-distance of screen from the slits). At a point P on the screen resulting intensity is equal to the intensity due to individual slit . Then the distance of point P from the central maxima is (
View SolutionIn Young's double slit experiment (d)/(D) = 10^(-4) (d = distance between slits, D = distance of screen from the slits) At a point P on the screen the resulting intensity is equal to the intensity due to individual slit I_(0) .Then the distance of point P from the central maximum is (lambda = 6000 Å) :
View SolutionIn Young's double-slit experiment d//D = 10^(-4) (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit I_(0) . Then, the distance of point P from the central maximum is (lambda = 6000 Å)
View SolutionIn a Young's double-slit experiment with light of wavelength , the separation of slits is d and distance of screen is D such that . If the Fringe width is , the distance from point of maximum intensity to the point where intensity falls to half of maximum intensity on either side is :
View SolutionLight of wavelength lambda is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is ––
View SolutionLight of wavelength is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is
View SolutionIn a Young's double slit experiment, d=1 mm, lambda =6000 Å and D-1 m(where d, lambda and D have usual meaning). Each of slit individually produces same intensity on the screen. The minimum distance between two points on the screen having 75% intensity of the maximum intensity is
View SolutionIn a Young's đouble slit experiment, d=1 mm, lambda=6000 A and D=1m (where d, lambda and D have usual meaning). Eachof slit individually produces same intensity on the screen. The minimum distance between two points on the screen having 75 % intensity of the maximum intensity is in mm.
View SolutionWhich two figure have an equal area? (FIGURES) and (b) and (c) and (d) and
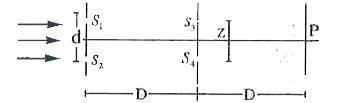
View SolutionConsider the arrangement shown in figure, By some mechanism, the separation between the slits and can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of and . When , the intensity measured at P is I. Find this intensity when z is equal to 1) , (2) and (3) .
View SolutionIn a Young's double slit experiment, d = 1mm, and D-1 m (where d, , and have usual meaning). Each of slit individually produces same intensity on the screen. The minimum distance between two points on the screen having 75% intensity of the maximum intensity is
View SolutionIn YDSE, having slits of equal width, let be the fringe width and be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be
View Solution