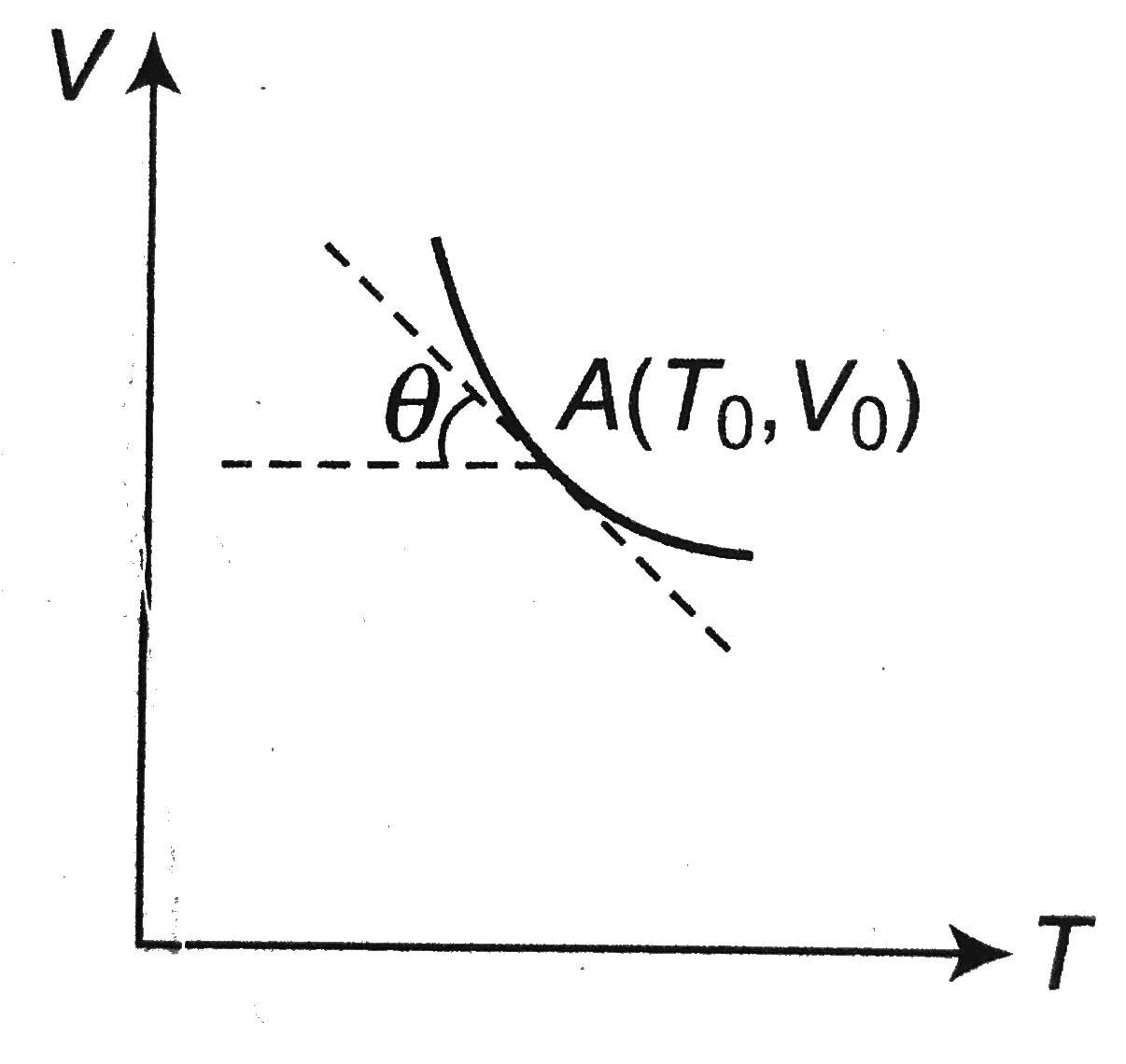
A gas is undergoing an adiabatic process. At a certain stage A the values of volume and temperature = V0 T0 and the magnitude of the slope of V-T curve is m. Find the value of Cp and CV.
PVγ = constant
Related Solutions
For a gas undergoing an adiabatic process, at a certain stage its volume and temperature are V_0, T_0 and the magnitude of slope of V - T curve is in
View SolutionA gas is undergoing an adiabatic process. At a certain stage, the volume and absolute temperature of the gas are V_(0), T_(0) and the magnitude of the slope of the V-T curve is m. molar specific heat of the gas at constant pressure is [Assume the volume of the gas is taken on the y-axis and absolute temperature of the gas taken on x-axis]
View SolutionA gas is undergoing an adiabatic process. At a certain stage, the volume and absolute temperature of the gas are V_(0), T_(0) and the magnitude of the slope of the V-T curve is m. molar specific heat of the gas at constant pressure is [Assume the volume of the gas is taken on the y-axis and absolute temperature of the gas taken on x-axis]
View SolutionA gas is undergoing an adiabatic process. At a certain stage A, the values of volume and temperature . From the details given in the graph, find the value of adiabatic constant
View SolutionOn P-V coordinates, the slope of an isothermal curve of a gas at a pressure P = IMPa and volume V= 0.0025 is equal to . If , the slope of the adiabatic curve passing through this point is :
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as , then the value of for the gas is
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T prop V^(-(3)/(4)) , then the value of (C_(P))/(C_(V)) for the gas is
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as , then the value of for the gas is
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as , then the value of for the gas is
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT^(2)= constat where V= volume of gas, T= temperature of gas. Then under process
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT^(2)= constat where V= volume of gas, T= temperature of gas. Then under process
View SolutionWhen a polyatomic gas undergoes an adiabatic process, its temperature and volume are related by the equation TI^(-1) =constant, the value of n will be
View SolutionWhen a polyatomic gas undergoes an adiabatic process, its temperature and volume are related by the equation =constant, the value of will be
View SolutionWrite the relation between volume and temperature of an ideal gas undergoing an adiabatic process.
View Solutionरुद्धोष्म प्रसार से गुजरने वाली एक आदर्श गैस का ताप, आयतन के साथ के अनुसार परिवर्तित होता है, तो गैस के लिए का मान ज्ञात कीजिए।
View SolutionA gas may expands either adiabatically or isothermally. A number of p-V curves are drawn for the two process over different ranges of pressure and volume. It will be found that a) Two adiabatic curves do not intersect b) Two isothermal curves do not intersect c) An adiabatic curve and an isothermal curve may intersect d) The magnitude of the slope of an adiabatic curve is greater than the magnitude of the slope of an isothermal curve for the same values of pressure and volume
View SolutionA gas may expand either adiabatically or isothermally. A number of p-V curves are drawn for the two process over different ranges of pressure and volume. It will be found that a) Two adiabatic curves do not intersect b) Two isothermal curves do not intersect c) An adiabatic curve and an isothermal curve may intersect d) The magnitude of the slope of an adiabatic curve is greater than the magnitude of the slope of an isothermal curve for the same values of pressure and volume
View SolutionFigure shows a parabolic graph between T and (1)/(V) (T = temperature, V = Volume) for a gas undergoing an adiabatic process. If the ratio of rms velocity of molecules and speed of sound in the gas at the same temperature is sqrtn , then find the value of n.
View SolutionFigure shows a parabolic graph between T and (1)/(V) (T = temperature, V = Volume) for a gas undergoing an adiabatic process. If the ratio of rms velocity of molecules and speed of sound in the gas at the same temperature is sqrtn , then find the value of n.
View SolutionA gas expands adiabatically at constant pressure,such that its temperature Where is Volume then the value of of the gas is ?
View Solution