The work done on the gas in taking it from D to A isA – 414 R B + 414 R C – 690 R D + 690 R
Correct option A – 414 R Explanation At constant temperature isothermal process
Related Solutions
If is a parallelogram, then prove that
View SolutionIf is a parallelogram, the prove that =1/2a rA B C D)
View SolutionIS A PARALLELOGRAM AND is any point in its interior. Prove that: Given: A parallelogram is a point in its interior. To Prove:
View SolutionLet A = {a,b,c,d} and R = {(a,b),(a,c),(a,d), (b,c), (b,d), (c,d)} then R =R is equal to
View Solutionis a parallelogram and is any point in its interior. Prove that:
(i)
(ii)
View SolutionIn Figure, is a point in the interior of a parallelogram . Show that
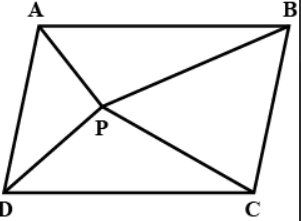
View SolutionIn Figure, is a point in the interior of a parallelogram . Show that
View SolutionLet be a relation on defined by then show that: for all
View SolutionIn Figure, is a point in the interior of a parallelogram Show that
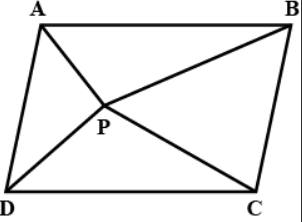
View SolutionIn Figure, is a point in the interior of a parallelogram Show that
View SolutionIf is a parallelogram, then prove that =
View SolutionLet R be a relation over the set NxxN and it is defined by (a,b)R(c,d)impliesa+d=b+c . Then R is
View SolutionLet R be a relation over the set NxxN and it is defined by (a,b)R(c,d)impliesa+d=b+c . Then R is
View SolutionAssertion: The scalar product of a force and displacement is equal to the work done.
Reason: Work done is not a scalar
(A) Both A and R are true and R is the correct explanation of A
(B) Both A and R are true R is not te correct explanation of A
(C) A is true but R is false.
(D) A is false but R is true.
View SolutionAssertion: The scalar product of a force and displacement is equal to the work done. Reason: Work done is not a scalar (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not te correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View Solutionis equal to (A) (B) (C) 11+r/R
View Solutionis a parallelogram whose diagonals intersect at If is any point on prove that:
View SolutionIn A ABC , P and Q are respectively the mid-points of and and R is the mid-point of Prove that:
View SolutionIn Fig.9.29, and . Show that both the quadrilaterals ABCD and DCPR are trapeziums.
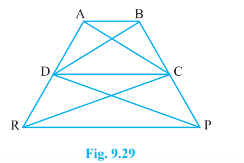
View SolutionIn Fig.9.29, and . Show that both the quadrilaterals ABCD and DCPR are trapeziums.
View Solution