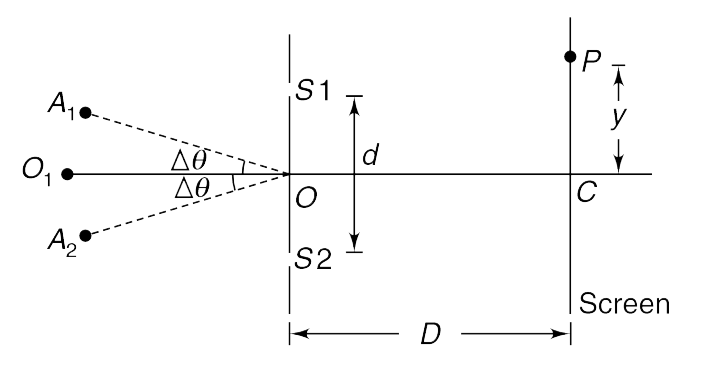
Two coherent sources S1 and S2 having same phase emit light of wavelength λ. The separation between S1 and S2 is 2λ. The light is collected on a screen placed at a distance D > > λ from slit S1 as shown in figure. Find the minimum distance so that the intensity at P is equal to intensity at O. a D/√2b √2 Dc D/√3d D√3
Correct option d D√3Explanation:
Related Solutions
In a young’s double slit experiment the distance between slits S1 and S2 is d and distance of slit plane from the screen is . The point source of light (S) is placed a distance below the principal axis in the focal plane of the convex lens (L). The slits S1 and S2 are located symmetrically with respect to the principal axis of the lens. Focal length of the lens is .
Find the distance of the central maxima of the fringe pattern from the centre (O) of the screen.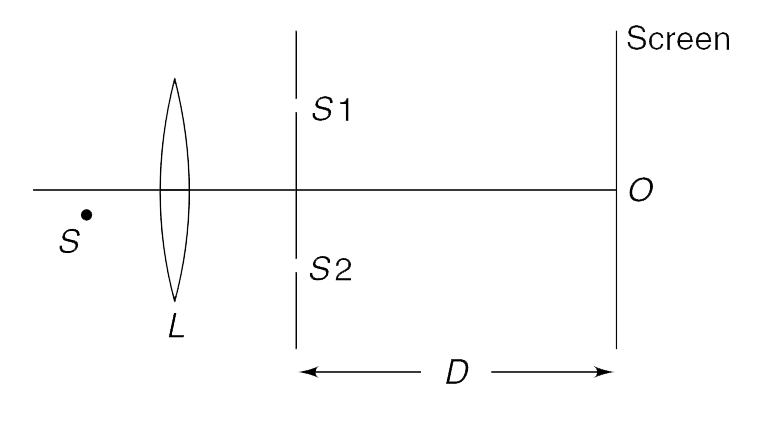
View SolutionIn the shown fig. S1 and S2 are two identical coher- ent sources of sound, separated by a distance d. A receiver moves along the line XY (which is parallel to line S1 S2) to detect the intensity of sound at various points on the line. Distance of line XY from line S1 S2 is. Point O is the foot of perpendicular bisector of the line S1 S2 on XY. Distance of first intensity maxima (on line XY) measured from O is y. Find percentage change in value of y if the temperature of air increases by 1%.
View SolutionTwo coherent point sources S_1 and S_2 vibrating in phase emit light of wavelength lamda . The separation between them is 2lamda . The light is collected on a screen placed at a distance Dgt gt lamda from the slit S_1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
View Solutiontwo art allied point sources S_(1) And S_(2) Vibrating in art, emit light of wavelength. distance between them 2lambda Is. slit as shown S_(1) distance from D gt gt lambda Light is collected on a screen placed on The minimum distance, so that the intensity at P is equal to the intensity at O, is:
View SolutionTwo coherent narrow slits emitting sound of wavelength lamda in the same phase are placed parallel to each other at a small separation of 2lamda . The sound is detected by moving a detector on the screen sum at a distance D(gtgtlamda) from the slit S_1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
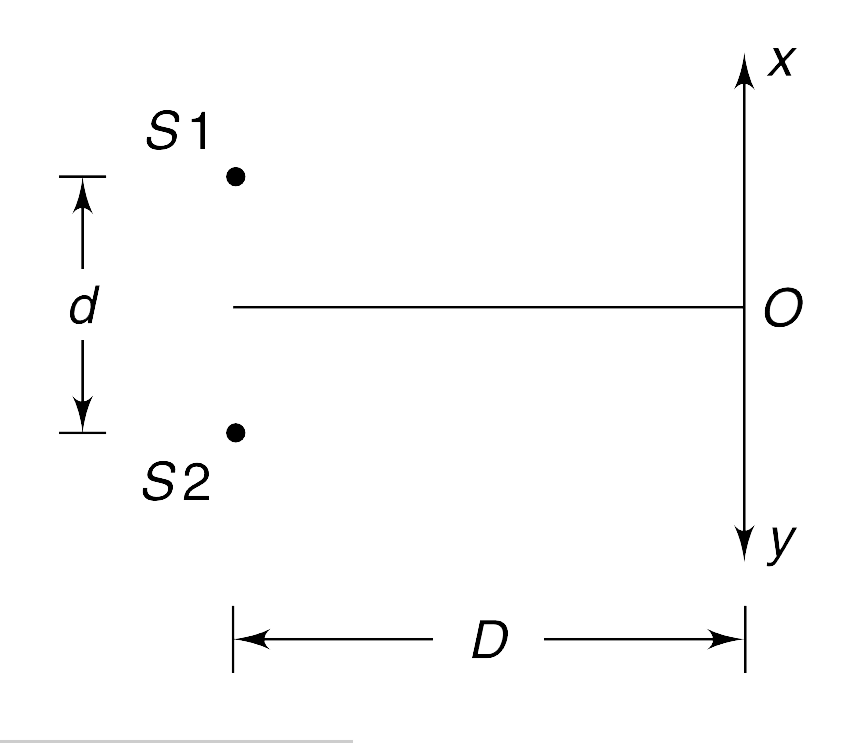
View SolutionIn the arrangement shown in the figure, S1 and S2 are two parallel slits at a separation d. There is a screen at a distance from the slits. Two point sources A1 and A2 have been placed symmetrically with respect to the slits at a large distance with. The sources are monochromatic giving out light of wavelength l but they are incoherent. Write the intensity of light at a point P on the screen as a function of y. Take to be maximum intensity on the screen when one of the two sources (A1 and A2) is switched on. Assume y to be small.
View SolutionIn Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
View SolutionDiscussion Sheet S1 and S2
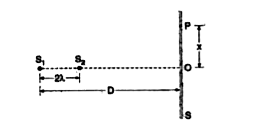
View SolutionTwo coherent narrow slits emitting light of wavelength in the same phase are placed parallel to each other at a small separation of The light is collected on a screen S which is placed at a distance from the slit as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity at O.
View SolutionA point source of light 'S' at a distance d from the screen A produces light intensity at the centre of the screen. If a completely reflecting mirror M is placed at a distance d behind the source as shown in the figure, find the intensity at the centre of the screen

View SolutionChoose the most appropriate option. Two coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda . The separation between them is 2lambda . The light is collected ona screen placed at a distance D gt gt lambda from the slit S_(1) as shown. The minimum distance, so that intensity at P is equal to intensity at O.
View SolutionTwo coherent narrow slits emitting light of wavelength in the same phase are placed to each other at a small separation of . The light is collected on a screen S which is placed at a distance from the slit as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity at O.
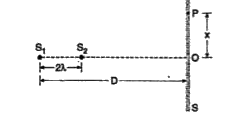
View SolutionTwo coherant narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda .The light is collected on a screen S which is placed at a distance D( gt gt A) from the slit S_(1) as shown in figure .Find teh finite distance x such that the intensity of P is equal to intensity at O .
View SolutionTwo coherent narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda . The light is collected on a screen S which is placed at a distance D(gtgt lambda ) from the slit S_1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O. .
View SolutionTwo coherent narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda . The light is collected on a screen S which is placed at a distance D(gtgt lambda ) from the slit S_1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O. .
View SolutionTwo coherent narrow slits emitting light of wavelength lamda in the same phase are placed parallel to each other at a small separation of 3lamda the light is collected on a screen S which is placed at a distance D(gt gt lamda) from the slits the smallest distance x such that the P is a maxima.
View SolutionTwo coherent narrow slits emitting light of wavelength lamda in the same phase are placed parallel to each other at a small separation of 3lamda the light is collected on a screen S which is placed at a distance D(gt gt lamda) from the slits the smallest distance x such that the P is a maxima.
View SolutionConsider the situation shown in figure. The two slite S_1 and S_2 placed symmetrically around the centre line are illuminated by a monochromatic light of wavelength lambda. The separation between the slits is d. The light transmitted by the slits falls on a screen M_1 placed at a distance D from the slits. The slit S_3 is at the centre line and the slit S_4 is at a distance y form S_3 . Another screen M_2 is placed at a further distance D away from M_1 . Find the ration of the maximum to minimum intensity observed on M_2 if y is equal to (dltltD) .
View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is and I is the intensity of central bright fringe, then intensity at distance from central maximum is
View SolutionThe intensity at the maximum in Young's double slit experiment is I_0 Distance two slits is d = 5lambda where lambda is the wavelength of light used in the experiment what will be intensity in front of one of the slits on the screen placed at a distance D=10d ?
View Solution