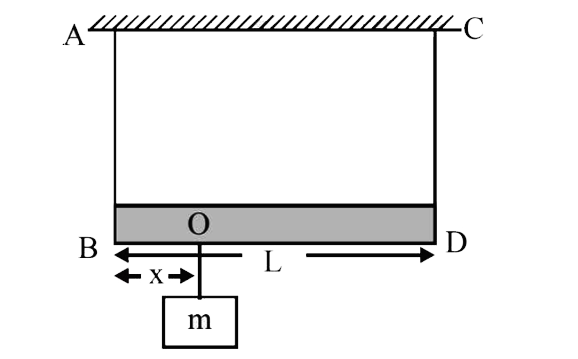
A massless rod is suspended by two identical strings AB and CD of equal length Fig. 8.15. A block of mass m is suspended from point O such that BO is equal to x. Further it is observed that the frequency of 1st harmonic fundamental frequency in AB is equal to 2nd harmonic frequency in CD. Then length BO is a L/5 b 4L/5 c 3L/4 d L/4
Let T1 and T2 be tensions in two strings AB and CD respectively. ThenTaking torque about O for equilibrium we haveCorrect Choice : a.
Related Solutions
A massless rod is suspended by two identical strings AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to ‘x’. Further, it is observed that the frequency of 1^st harmonic (fundamental frequency) in AB is equal to 2^nd harmonic frequency in CD. Then, length of BO is
View SolutionA massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to 'x'. Further it is observed that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD . 'x' is
View SolutionA massless rod of length is suspened by two identical string and of equal length. A block of mass is suspended from point such that is equal to 'x'. Further it is observed that the frequency of harmonic in is equal to harmonic frequency in . 'x' is
View SolutionA massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal ti 'x'. Further it is obsreved that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD . 'x' is
View SolutionA massless rod of length l of length BD is suspended by two identical massless strings AB and CD of equal length. A block of mass m is suspended from a point P such that BP is equal to x. If the original frequency of the left string is twice the original frequency of the right string, then l/x The value of:
View SolutionA weightless rod is hung by two equal lengths of equal ropes AB and CD. A mass m hangs from point O such that BO = x. By observation, it is known that the frequency of the first sound in AB is equal to the frequency of the second sound in CD, then the length of BO is
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
View SolutionSame length and two threads AB And CD A weightless rod hangs from a m Point of mass block O From a type that is hung BO The length is x. The observer knows that AB When the frequencies of the first sound are equal BO Is the length of
View Solutionएक द्रव्यमान छड़ BD को एक जैसी द्रव्यमानहीन डोरियों AB तथा CD द्वारा लटकायी गई है। m द्रव्यमान का एक ब्लॉक बिन्दु P से लटकाया गया है जहाँ दुरी RP , (AB = CD) x के बराबर है। यदि दायीं डोरी कि मूल आवृत्ति बायीं डोरी कि मूल आवृत्ति से दोगुनी है , तब x का मान है।
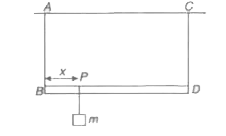
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png)
View SolutionA uniform rod AB of mass m and length l is suspended by two massless and inextensible strings AC and BD whose ends C and D are fixed as shown. Find the tension in the string BD immediately after the string at A is cut.
View SolutionA particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed omega with rod as the axis.
View SolutionA point mass m is suspended from the end of a massless wire of length L and cross section A. If Y is the Young's modulus for the wire, then the frequency of oscillations for simple harmonic motion along the vertical line is:
View SolutionFundamental frequency of an open pipe of length 0.5 m is equal to the frequency of the first overtone of a closed pipe of length l . The value of l_(c) is (m)
View SolutionThe fundamental frequency of a closed pipe is equal to the frequency of the second harmonic of an open pipe. The ratio of their lengths is
View SolutionThe fundamental frequency of a closed pipe is equal to the frequency of the second harmonic of an open pipe. The ratio of their lengths is
View SolutionA uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :

View SolutionA mass m is suspended from a spring of length l and force constant K . The frequency of vibration of the mass is . The spring is cut into two equal parts and the same mass is suspended from one of the parts. The new frequency of vibration of mass is . Which of the following relations between the frequencies is correct
View Solution