Let a and b be two integers such that 10 a + b = 20 and gx = x2 + ax + b. If g10 g11 = gn then n is equal toA 110 B 120 C 130 D 140
Correct option C 130Explanation:g10 g11 = gn 100 + 10a + b 121 + 11a + b = n2 + an + b 100 + 20 121 + 10a + b + a = n2 + an + 20 – 10a 120 141 + a = n2 + 20 + an – 10 120 . 141 + 120a = n2 + 20 + n – 10a on comparison n – 10 = 120 n = 130n2 + 20 = 120.141
Related Solutions
Find the polymer of the data given below - 110, 120, 130, 120, 110, 140, 130, 120, 140, 120, 110, 115, 130, 120
View SolutionFind the mode from the following data : 110, 120, 130, 120 I 110, 140, 130, 120, 140, 120.
View Solutionनिम्न आँकड़ो का बहुलक (mode) ज्ञात करो :
110, 120, 130, 120, 110, 140, 130, 120, 140, 120
View SolutionFind the mode from the following data: 110, 120, 130, 120, 110, 140, 130, 120, 140, 120
View SolutionFind the mode of the following data: 120, 110, 130, 110, 120, 140, 130, 120, 140, 120
View SolutionFind the mode of the following data: 120, 110, 130, 110, 120, 140, 130, 120, 140, 120
View SolutionLet a and b be two integers such that 10a+b=20 and g(x)=x^(2)+ax+b is equal to
View SolutionLet a and b be two integers such that If then n is equal to
View Solutionएक परीक्षा में और के अंकों का योग 120 है, और का 130 है तथा और का 140 है तो के अंक कितने हैं?
View SolutionIn an exam the sum of the scores of A and B is 120, that of B and C is 130 and that of C and A is 140. Then the score of C is:
View SolutionLet a and b be two integers such that 10a+b=20 and g(x)=x^(2)+ax+b. If g(10)g(11)=g(n), then n is equal to
View SolutionLet A and B be two sets such that n(A)= 70, n(B)=60 and n(AB) = 110. Then n(AB) is equal to
View SolutionIn Figure, if and the value of is (b) (c) (d)
View SolutionIn Figure, if and the value of is
(a)
(b)
(c)
(d)
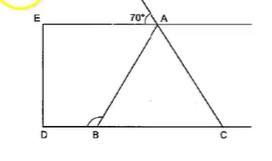
View SolutionIn the given figure, the value of are
(a)
(b)
(c)
(d)
View SolutionLet . Then n[(A xx B)nn(Bxx A ) equals to
View SolutionFind the derivative of (ax + b)^m (cx + d)^n , where a,b,c and d are constants and m,n are integers .
View SolutionThe class mark of the class interval is...a) b) c) d)
View SolutionIn Fig.67, the value of (b) (d)
View SolutionIn Fig.67, the value of (b) (d)
View Solution