A white pool ball m1 = 0.3 kg moving at a speed of vo1 = +3 m/s collides head-on with a red pool ball m2 = 0.4 kg initially moving at a speed of vo2 = - 2 m/s. Neglecting friction and assuming the collision is perfectly elastic what is the velocity of each ball after the collision?
The sketches below represent the system before and after the collisionSince momentum is conserved in this collision we can set the total momentum of the system before the collision equal to the total momentum after the collision:But here we have two unknowns vf1 and vf2 and only one equation. We can generate another equation containing the same variables if we remember that both momentum and kinetic energy are conserved in an elastic collision. Substituting the equation solved above for vf1 into the equation for conservation of kinetic energy we get one equation with only one unknown namely vf2. Substituting the known values into this equation and solving for vf2 gives vf2 = +2.3 m/s. Solving for vf1 in the equation above gives vf1 = - 2.7 m/s.It can be shown that if we solve the equations for conservation of momentum and conservation of kinetic energy simultaneously it always turns out that the relative speeds of the two masses remains the same except for a negative sign before and after a perfectly elastic collision regardless of the masses of the two objects. That is v01 − v02 = − vf1 − vf2 Collisions in Two Dimensions
Related Solutions
A ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at angle of 30^@ with the original line of motion. Assuming that the collision is elastic, what are the speeds of the balls after the collision?
View SolutionA ball weighing 2 kg and speed collides with another ball of 4 kg moving in opposite direction with speed of . They combine after the collision. The speed of this combined mass (in ) is :
View SolutionA ball weighing 2 kg and speed collides with another ball of 4 kg moving in opposite direction with speed of . They combine after the collision. The speed of this combined mass (in ) is :
View SolutionA highly elastic ball moving at a speed of approaches a wall moving towards it with a speed of . After the collision. the speed of the ball will be
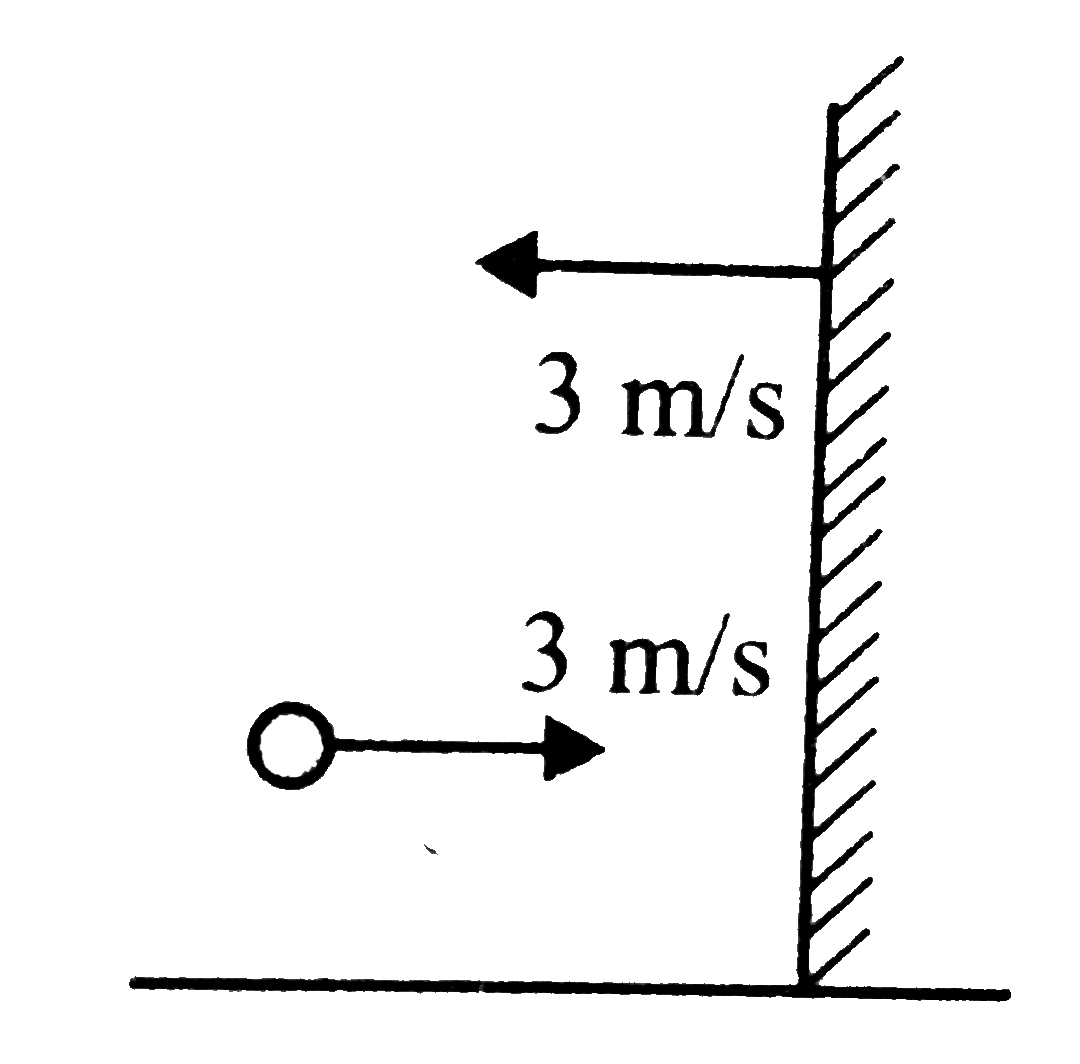
View SolutionA highly elastic ball moving at a speed of 3 m//s approaches a wall moving towards it with a speed of 3 m//s . After the collision. the speed of the ball will be
View SolutionA ball moving with speed u collides with an identical ball at rest. The velocities of two balls after collision are (If the collision is elastic):
View SolutionA ball collides elastically with another ball of the same mass. The collision is oblique and initially one of the balls was at rest. After the collision, the two balls move with same speeds. What will be the angle between the velocity of the ball after the collision?
View SolutionA ball collides elastically with another ball of the same mass. The collision is oblique and initially one of the balls was at rest. After the collision, the two balls move with same speeds. What will be the angle between the velocity of the ball after the collision?
View SolutionA ball A of mass 1 kg , moving with a speed of 12 m//s , collides obliquely and elasticity with another ball B which was initially at rest. Ball A then moves off at the right angle to its initial direction with a speed of 5 m//s . The momentum of ball B after the collision is
View SolutionTwo balls roll toward each other. The red ball has a mass of 0.5 kg and a speed of 4m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2 m/s. if the collision is perfectly inelastic, determine the velocity of the composite object after the collision.
View Solution9 मीटर/सेकंड की चाल से गतिमान 0.1 किग्रा द्रव्यमान की एक गेंद , एक दूसरी उसी द्रव्यमान की स्थिर गेंद से टकराती है । यदि टक्कर के पश्चात प्रत्येक गेंद प्रारंभिक गति की दिशा से का कोण बनाते हुए जाती है , तो उनके टक्कर के बाद वेग ज्ञात कीजिए । यह भी बताइये कि यह संघट्ट प्रत्यास्थ है अथवा अप्रत्यास्थ ?
View Solution1 kg द्रव्यमान की एक गेंद जो के वेग के साथ गतिमान है, एक अन्य स्थिर गेंद से टकराती है। संघट्ट के बाद, पहली गेंद अपनी प्रारंभिक दिशा के साथ का कोण बनाते हुए वेग के साथ गति करती है। संघट्ट के बाद दूसरी गेंद का संवेग होगा ( में)
View SolutionTwo balls roll towards each other. The red ball has a mass kg 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2m/s. after the head-on collision, the red ball continues forward with a speed of 2m/s. find the speed of the green ball after the collision. was the collision elastic?
View SolutionTwo identical balls A and B moving with velocities + 0.5 m/s and -0.3 .m/s respectively collide head-on elastically. The velocities of the ball A and B after collision will be respectively
View SolutionA ball of mass 5 kg moving with speed 8 m/s collides head on with another stationary ball of mass 15 kg. If collision is perfectly inelastic, then loss in kinetic energ is
View SolutionA ball of mass 5 kg moving with speed 8 m/s collides head on with another stationary ball of mass 15 kg. If collision is perfectly inelastic, then loss in kinetic energ is
View SolutionA ball moving with velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of 30^(@) with the original line of motion. What are the speeds of the balls after the collision ?
View SolutionA ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collisions each ball moves at an angle of 30^(@) with the original line of motion. What are the speeds of the balls after the collision?
View SolutionA ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of 30^@ with the original line of motion. What are the speeds of the balls after the collision?
View SolutionA ball , moving at , collides head - on with a ball moving in the opposite direction at . If the coefficient of restitution is , then the energy lost in the collision is
View Solution