Consider curve y = fx then if PT = Length of tangent PN = Length of normal TM = Length of subtangent MN = Length of sub normal thenA TM . MN = fxB PT/PN = 1/fxC PT . PN = constantD PT . TM = constant
Correct option BExplanation:
Related Solutions
The given curve is y = f (x), then If PT = Length of tangent line PN = Length of Perpendicular TM = Length of Asbestos MN = length of perpendicular, then
View SolutionConsider curve then if PT = Length of tangent PN= Length of normal TM=Length of subtangent MN=Length of sub normal, then (a) (b) (c) (d)
View SolutionConsider curve then if PT = Length of tangent PN= Length of normal TM=Length of subtangent MN=Length of sub normal, then (b) (d)
View SolutionLet P (h,K) be any point on curve Let tangent drawn at point P meets x-axis at T & normal at point P meets x-axis at N (as shown in figure) and m = shope of tangent.

(i) Length of tangent =PT
(ii) Length of Normal =PN +
(iii) Length subtangent = Projection of segment PT on x-axis
(iv) Length of subnormal =Projection of line segment PN on x-axis =MN
Find the product of length of tangent and length of normal for the curve at point x=0
View SolutionLet P (h,K) be any point on curve Let tangent drawn at point P meets x-axis at T & normal at point P meets x-axis at N (as shown in figure) and m = shope of tangent.

(i) Length of tangent =PT
(ii) Length of Normal =PN +
(iii) Length subtangent = Projection of segment PT on x-axis
(iv) Length of subnormal =Projection of line segment PN on x-axis =MN
Find the product of length of tangent and length of normal for the curve at point x=0
View SolutionConsidered two ellipses of ellipse F_(1),F_(2) Are and at point P then PT and PN are tangent line and normal respectively.
View SolutionLet P (h,K) be any point on curve Let tangent drawn at point P meets x-axis at T & normal at point P meets x-axis at N (as shown in figure) and m = shope of tangent.

(i) Length of tangent =PT
(ii) Length of Normal =PN +
(iii) Length subtangent = Projection of segment PT on x-axis
(iv) Length of subnormal =Projection of line segment PN on x-axis =MN
Determine 'p' such that the length of the subtangent and subnormal is equal for the curve at the point (0,1)
View SolutionLet P (h,K) be any point on curve Let tangent drawn at point P meets x-axis at T & normal at point P meets x-axis at N (as shown in figure) and m = shope of tangent.

(i) Length of tangent =PT
(ii) Length of Normal =PN +
(iii) Length subtangent = Projection of segment PT on x-axis
(iv) Length of subnormal =Projection of line segment PN on x-axis =MN
Determine 'p' such that the length of the subtangent nad subnormal is equal for the curve at the point (0,1)
View SolutionLet P (h,K) be any point on curve Let tangent drawn at point P meets x-axis at T & normal at point P meets x-axis at N (as shown in figure) and m = shope of tangent.

(i) Length of tangent =PT
(ii) Length of Normal =PN +
(iii) Length subtangent = Projection of segment PT on x-axis
(iv) Length of subnormal =Projection of line segment PN on x-axis =MN
Find length of subnormal to
View SolutionLet be two focii of the ellipse and be the tangent and the normal respectively to the ellipse at ponit P.then
View SolutionLet be two focii of the ellipse and be the tangent and the normal respectively to the ellipse at ponit P.then
View SolutionLet be two focii of the ellipse and be the tangent and the normal respectively to the ellipse at ponit P.then
View SolutionIf from any point P, tangents PT, PT' are drawn to two given circles with centres A and B respectively, and if PN is the perpendicular from P on their radical axis, then =
View SolutionIn the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
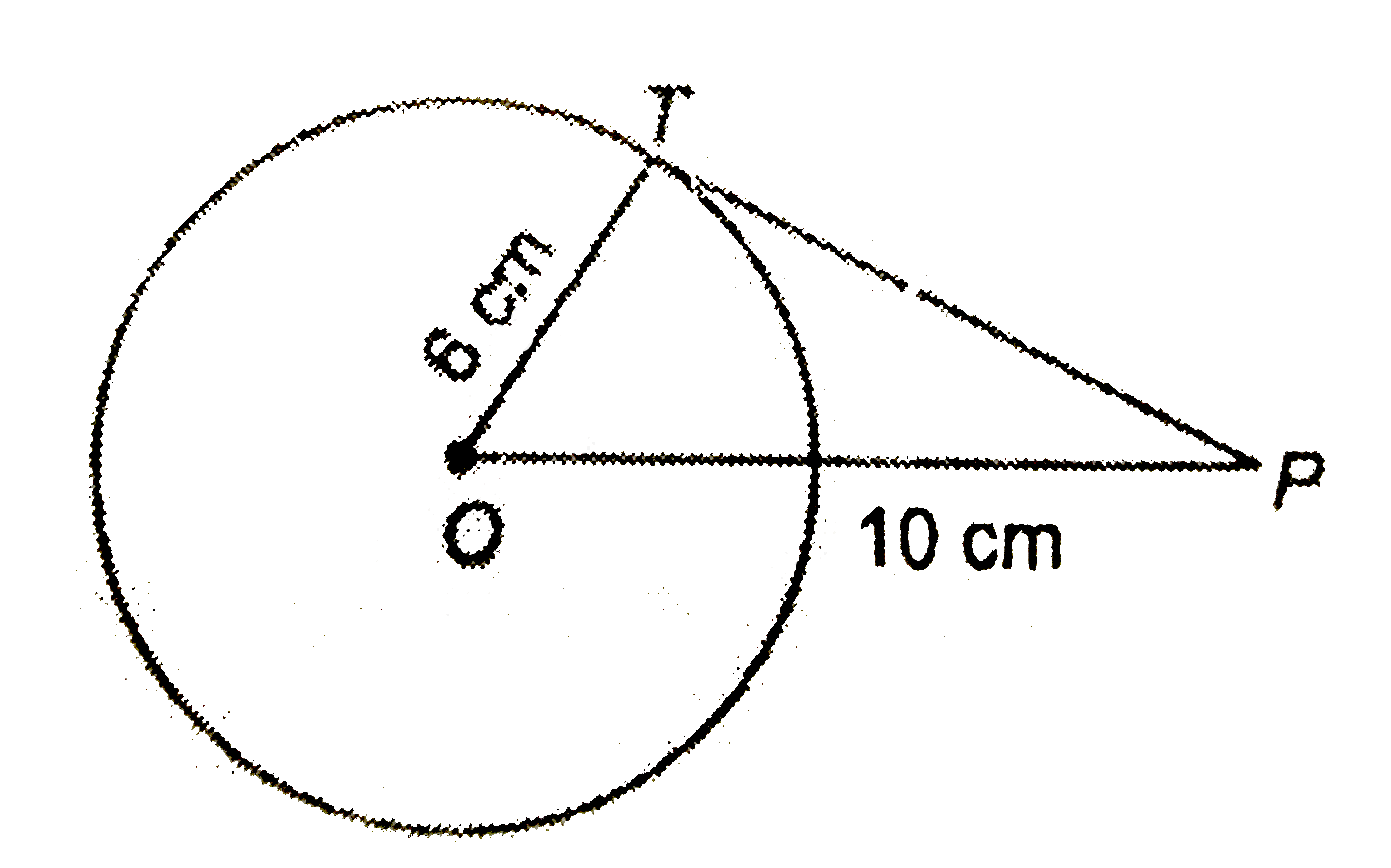
View SolutionIn the adjoining figure,PT is tangent to a circle with centre O.if OP= 25cm and radius of circle is 7cm ,then find the length of the tangent PT.
View SolutionPT दिए गए चित्र में O केंद्र वाले वृत्त की एक स्पर्श रेखा है| यदि OT=6 cm और OP=10 cm, तब स्पर्श रेखा PT की लम्बाई है:
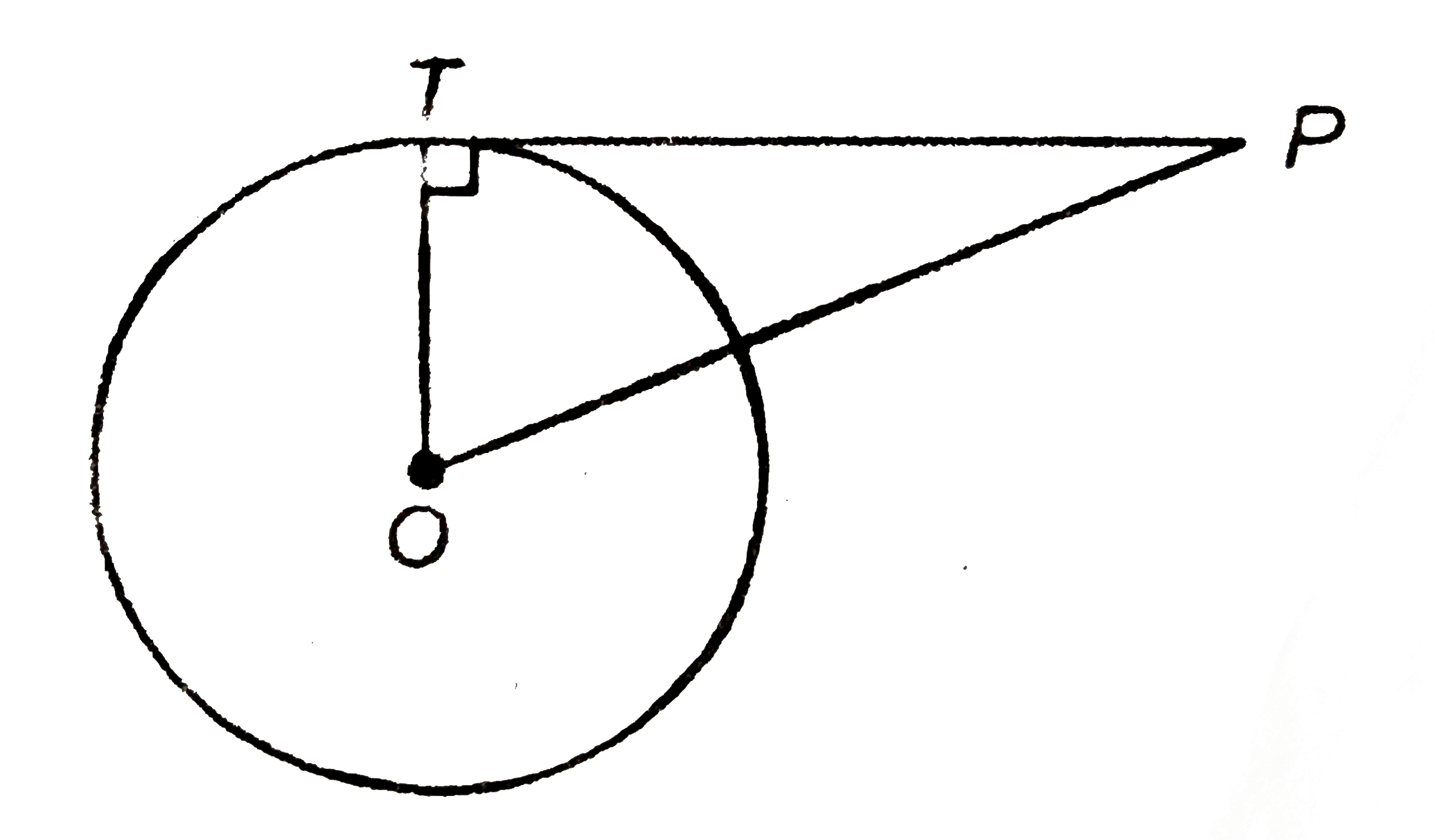
View SolutionIf is a tangent at to a circle whose centre is and , , Find the length of the tangent segment .
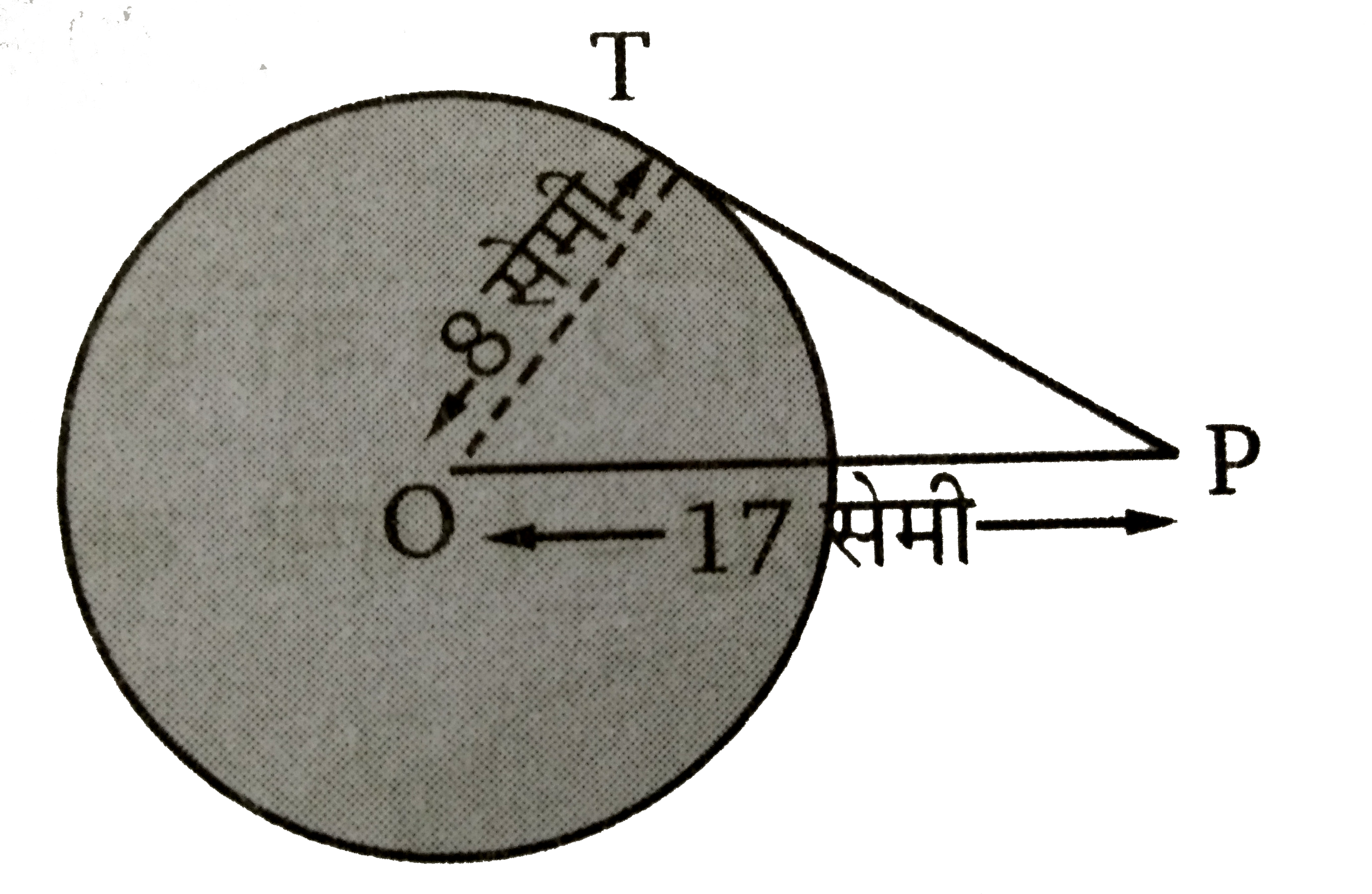
View Solutionचित्र में PT, O केन्द्र वाले वृत्त की स्पर्शी है। यदि OP = 17 सेमी तथा OT = 8 सेमी तब स्पर्शी PT की लम्बाई ज्ञात कीजिए ।
View SolutionIn the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
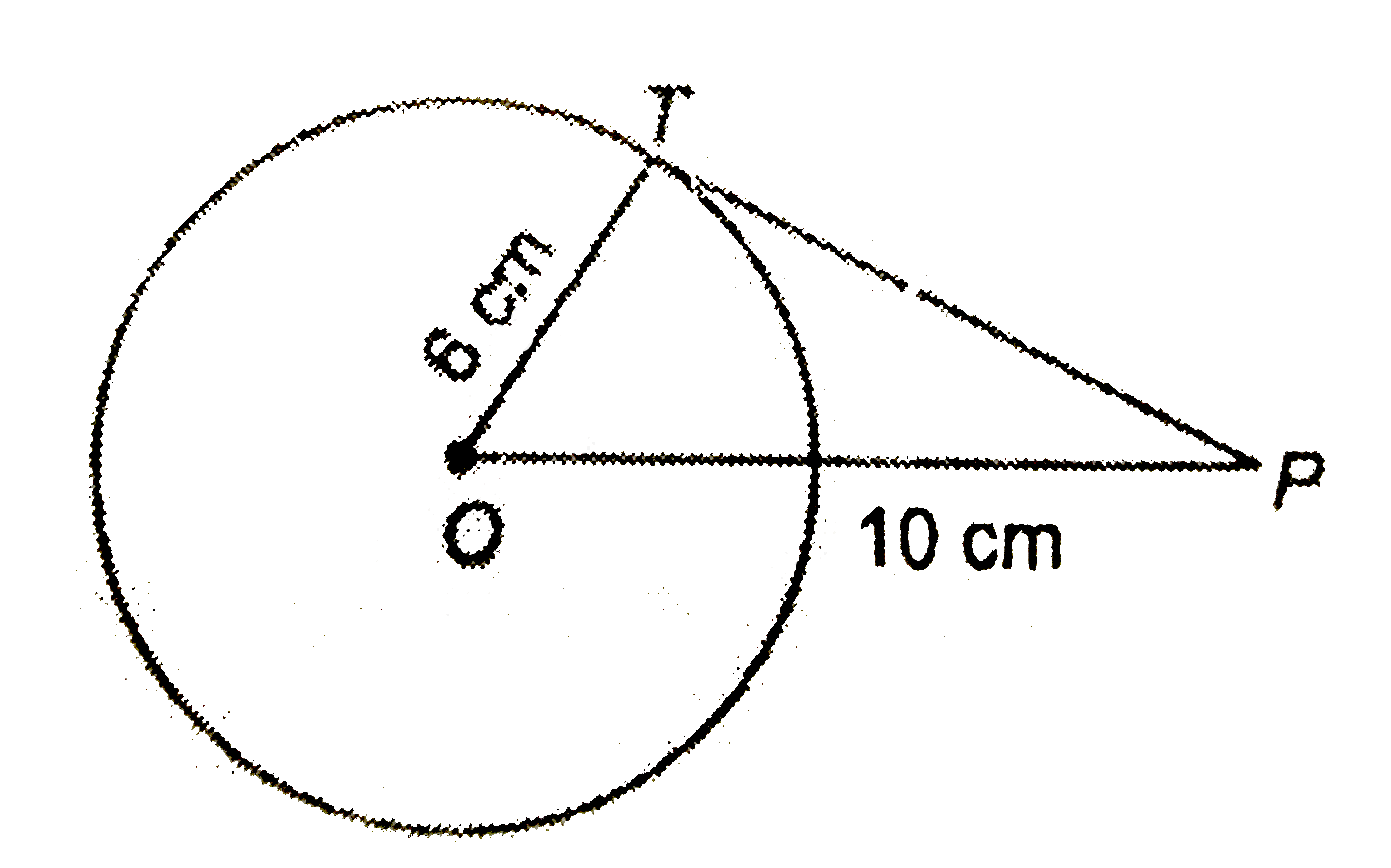
View SolutionFor the curve prove that (length of normal)^2/(length of tangent)^2 =length of sub-normal/length of sub-tangent
View Solution