A parallel beam of light is incident normally on the flat surface of a hemisphere of radius R = 6 cm and refractive index 1.56. Assuming paraxial ray approximation a determine the point at which the beam is focussed as measured along the axis from the curved surface; b determine the new focal length measured from the flat surface if the rays are incident at the curved surface
Rays pass without deviation at flat surfaces. From single surface refraction equation for single surface refraction equation for surface S2 we have 1/v – n/∞ = 1-n/-R v = R/n-1 = 6/[1.56-1] = 6/0.56 = 10.7 cm This focal point as rays travel from left. From single surface refraction equation at S1 we have n/v – 1/∞ = n-1/R v = nR/n-1 This is the first image it acts as an object for refraction at the plane surface. Object distance for refraction at S2 = [R/n-1]-R = R/n-1 so we have 1/v’- [n/+Rn-1] =0 v’ = R/nn-1 = 6/1.561.56-1 = 6.9 cm Hence focal point is at 6.9 cm from the plane surface.
Related Solutions
A parallel beam of light is incident normally on the flat surface of a hemisphere of radius 6 cm and refractive index 1.5 , placed in air as shown in figure (i). Assume paraxial ray approxiamtion. .
View SolutionA parallel beam of light is incident normally on the flat surface of a hemisphere of radius 6 cm and refractive index 1.5 , placed in air as shown in figure (i). Assume paraxial ray approxiamtion. .
View SolutionFrom the air on the flat surface of any liquid 45^@ The light rays incident at the corners are refracted from that surface 15^@ Is deviated. Determine the refractive index of the fluid.
View SolutionA parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :
View SolutionA parallel beam of monochromatic light is incident on the surface of water having refractive index 4/3. The direction of the incident beam bisects the angle between the normal to the water surface and the water surface. The angles of incidence and refraction are :
View SolutionA parallel beam of monochromatic light is incident on the surface of water having refractive index 4/3. The direction of the incidence beam bisects the angle between the normal to the water surface and the water surface. The angles of incidence and refraction are
View Solutionप्रकाश की एक समांतर किरण पुंज अभिलम्बवत रूप से एक समतल पृष्ठ पर आपतित होती है जो प्रकाश का 40 % भाग अवशोषित करती है और शेष भाग को परावर्तित करती है। यदि आपतित किरण 60 W शक्ति का वहन करती है, तो इसके द्वारा सतह पर लगाया गया बल है:
View Solutionएक बिन्दु प्रकाश-स्रोत से एक गोले की सतह पर समान्तर प्रकाश पुंज आपतित होता है और गोले की दूसरी सतह से निकल जाता है, तो गोले के पदार्थ का अपवर्तनांक होगा-
View SolutionA parallel beam of monochromatic light of frequency v is incident on a surface. Intensity of the beam is I and area of the surface is A. Find the force exerted by the light beam on the surface for following cases–
(i) the surface is perfectly absorbing and the light beam is incident normally on it.
(ii) the surface is perfectly reflecting and the light beam is incident normally.
(iii) the surface is perfectly absorbing and the light beam is incident at an angle of incidence .
(iv) the surface is perfectly reflecting and the light beam is incident at an angle of incidence .
View Solutionप्रकाश की समांतर बीम, किसी समतल काँच की सतह पर के कोण पर आपतित है और परावर्तित बीम, पूरी तरह ध्रुवित है।
(a) काँच में अपवर्तन कोण कितना है ?
(b) काँच का अपवर्तनांक कितना है ?
View Solutionप्रकाश है एक किरण काँच के समतल टुकड़े पर गिरती है जिसका अपवर्तनांक है|यदि परावर्तित किरण तथा अपवर्तित किरण अभिलंबवत है तो आपतन कोण ज्ञात कीजिये|
View SolutionA ray of light originating in oil (n=1.21) is incident at the Brewster angle upon a flat surface of a quartz crystal (n=1.458) . Determine the angle of incidence for this ray.
View SolutionA beam of light strikes a surface at angle of incidence of and reflected beam becomes completely polarised . The refractive index of glass surface is -
View SolutionA beam of light strikes a surface at angle of incidence of 60^(@) and reflected beam becomes completely polarised . The refractive index of glass surface is -
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
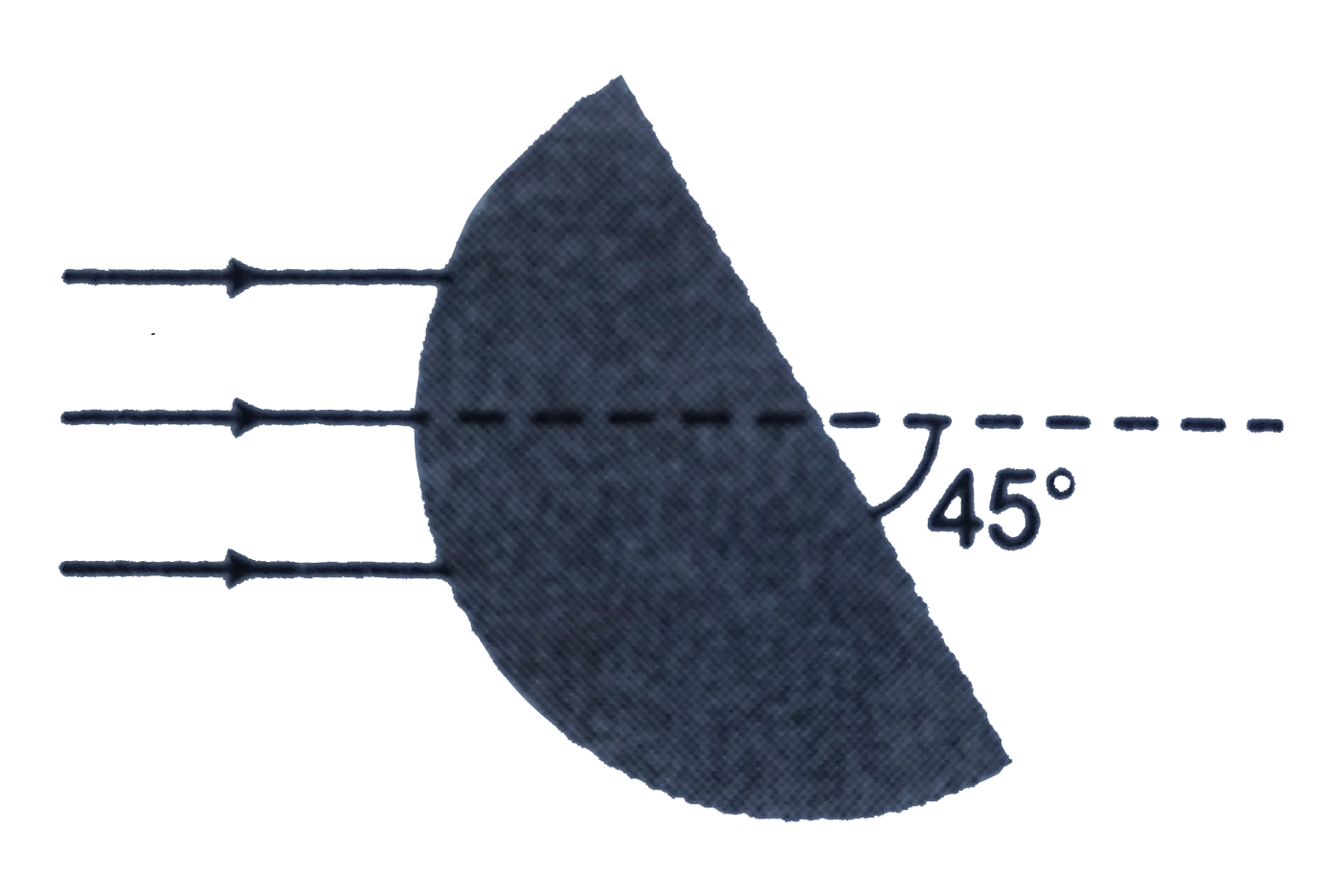
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as

View SolutionAn equiconvex lens of refractive index 1.5 and focal length 10 cm is held with its axis vertical and its lower surface immersed in water, the upper surface being in air. At what distance from the lens will a vertical beam of parallel rays incident on the lens be focussed? .
View SolutionA parallel beam of light is incident normally on a plane surface absorbing 40% of the light and reflecting the rest. If the incident beam carries 60W of power, the force exerted by it on the surface is
View SolutionA parallel beam of light is incident normally on a plane surface absorbing 40% of the light and reflecting the rest. If the incident beam carries 60W of power, the force exerted by it on the surface is
View SolutionA ray of light is incident on a refracting face of glass prism of refracting angle . If the ray emerges normally from the second refracting surface, the angle of incidence is refracting surface, the angle of incidence is
View Solution