Consider two convex lenses of focal lengths f1&f2 are made from same material are separated by a suitable distance d. The focal length of the combination is given by 1/f = 1/f1+1/f2-d/f1f2 the value of d for which combination is free from chromatic aberration is given bya f1+f2/2 b f1-f2/2 c f1+f2 d none
Consider two convex lenses of focal lengths f1&f2 separated by a suitable distance d. The focal length of the combination is given by: 1/f1+1/f2-d/f1f2 = 1/f 1 differentiate above equation -df1/f12 –df2/f22 –d[1/f1-df2/f22+1/ f2df1/f12] = -1/f2 df {df=0 for Achromatism} df1/f11/f1+df2/f21/f2 –d[df2/f21/f1f2 +df1/f11/f1f2]=0 ω1/f1 + ω2/f2 – d[ω2/f1f2 + ω1/f1f2] =0 ω1f2+ ω2f1/ f1f2 = dω2+ω1/ f1f2 which gives d = ω1f1+ ω2f2/ ω1+ω2 In case when lenses are of same material ω1 = ω2 = ω Then d = f1+f2/2 Thus two lenses of same nature can be free from chromatic aberration if they are placed at a separation d = f1+f2/2
Related Solutions
Two thin lenses of focal lengths f1 and f2, are in contact and coaxial. The power of combination is
View SolutionIf the two circle & touch each other than: (A) f1 g1 = f2 g2 (B) = (C) f1 f2 = g1 g2 (D) f1+ f2 = g1 + g2
View SolutionIn the figure given below there are two convex lenses L1 and L2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be
View SolutionConsider the following frequency distribution: What are the values of f1, and f2, respectively?
View SolutionState whether the following statements are True (T) or False (F):
The focal length of the new combined lens of f1 and f2 each are f is 2f.
View Solutionబాహుళకం సూత్రం = =నందు f1...... ను సూచించును.
View SolutionThe mean of the following frequency distribution is 50 Find f1 f2 f3 if f2 : f3 = 4 : 3:

View SolutionWhat shall be the genotypic ratio in generation of monohybrid cross?
View SolutionOn selfing a plant of F1 generation with genotype "AABbCC". the genotypic ratio in F2 generation will be
View Solutionવનસ્પતિમાં F1 પેઢીમાં જિનોટાઇપ AABbCC છે. આ વનસ્પતિમાં સ્વફલન થતાં F2 પેઢીમાં દેખાવ સ્વરૂપ પ્રમાણ .......છશે.
View SolutionF1 = 1, F2 = 3 மற்றும் Fn = Fn-1 + Fn-2 எனக் கொடுக்கப்படின் F5 ஆனது
View SolutionThe given bar graph represents the production and sales of certain crop in quintals by the farmers F1,F2,F3 and F4. Whatis the percentage less in the production by farmer F1 with respect to the production by farmer F2 ?
View Solutionएकसंतलिय बालों एवं एक्बिन्दुगामी बलों को परिभषित कीजिए। सिद्ध कीजिए की यदि कोई वस्तु किन्ही तीन बलों व के अधीन संतुलन में है तो
View SolutionThe given figure shows the plant of Commelina with two types of flowers (F1 and F2). The flowers
View SolutionF1, F2, F3, F4 and F5 are sitting on a bench. F4 sits to the immediate left of F2. F3 sits to the immediate right of F5. F1 is sitting at one of the corners and F2 has only one neighbour. Then who among the following friends is sitting in the middle with two friends at both the ends?
View SolutionThe production of gametes by the parents, formation of zygotes, the F1 and F2 plants, can be understood from a diagram called:
View SolutionThe production of gametes by the parents, formation of zygotes, the F1 and F2 plants, can be understood from a diagram called:
View SolutionWhich of the four arrangements in the figure correctly shows the vector addition of two forces F1 & F2 to yield the third force F_3?
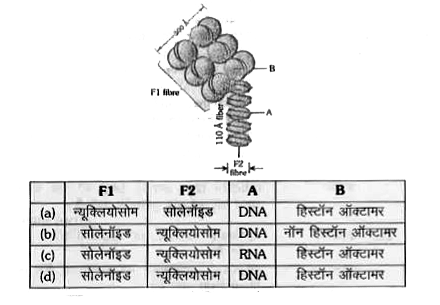
View Solutionदिया गया आरेख यूकैरियोट्स के क्रोमोसोम के आधारीय 30 mm रेशे की संरचना को दर्शाता है| सही विकल्प का चयन कीजिए जिसमें F1, F2, A तथा B सही निरूपित किए गए हो
View Solutionএকজন রুগির দৈনিক খাদ্যে অন্তত একক ভিটামিন এবং একক ভিটামিন- থাকা বাঞ্ছনীয়। দুই প্রকারের খাদ্য ও রুগির জন্য বরাদ্দ আছে। খাদ্যে একক ভিটামিন ও একক ভিটামিন আছে এবং গ্রাম খাদ্যের দাম পয়সা। খাদ্যে একক ভিটামিন ও একক ভিটামিন আছে এবং গ্রাম খাদ্যের দাম পয়সা।
কি পরিমানে ও খাদ্যে প্রয়োজনীয় ভিটামিন থাকবে এবং দাম সবচেয়ে কম হবে? সমস্যাটিকে রৈখিক প্রোগ্রামবিধি সমস্যারূপে প্রকাশ করো এবং লেখচিত্রের সাহায্যে সমাধান করো।
View Solution