If roots of the quadratic equation x + ax + 1991 + 1 = 0 are integer then a is equal to A 1989 B 1991 C 1993 D 1995
The correct Answer is:Option
Correct Option :- AExplanation :-
Related Solutions
If roots of the quadratic equation are integer, then is equal to (a is integer)
View SolutionThe sum of two numbers is 2000 and their L.C.M. is 21879. The two numbers are (a) 1993, 7 (b) 1991, 9 (c) 1989, 11 (d) 1987, 13
View SolutionThe value of is
View SolutionFind the all integers values of a such that the quadratic expressions can be factored as , where b and c are integers.
View SolutionThe number of integral values of a for which the quadratic equation has integral roots are a. b. c. d.
View SolutionThe number of integral values of a for which the quadratic equation has integral roots are a. b. c. d.
View SolutionThe number of integral values of a for which the quadratic equation (x+a)(x+1991)+1=0 has integral roots are a. 3 b. 0 c. 1 d. 2
View SolutionThe number of integral values of a for which the quadratic equation has integral roots are a. b. c. d.
View SolutionThe period (A)/between 1991 to 1995 (B)/was very significant in my life (C)/No error (D)/
View Solutionयदि समीकरण के मूल पूर्णांक है, तो 'a' का मान है-
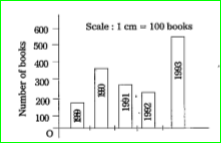
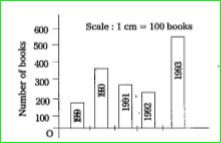
View SolutionHow many books were sold from 1989 to 1991?
View SolutionIf sum of the roots of the quadratic equation, , then the sum of the roots of the equation, is: (a) (b) (c) (d)
View SolutionHow many books were sold from 1991 to 1993?
View SolutionIf , such that are the roots of equation and are the roots of equation then is equal to
View SolutionIf a,b,c,d in R-{0} , such that a,b are the roots of equation x^(2)+cx+d=0 and c,d are the roots of equation x^(2)+ax+b=0, then |a|+|b|+|c|+|d| is equal to
View SolutionIn quadratic equation , if discriminant , then roots of quadratic equation are:
View SolutionIn quadratic equation , if discriminant , then roots of quadratic equation are:
View SolutionIn quadratic equation , if discriminant , then roots of quadratic equation are:
View SolutionIn quadratic equation , if discriminant , then roots of quadratic equation are:
View SolutionIf the quadratic equations, have a common root, then is equal to: a. -2 b. -2 c. 0 d. 1
View Solution