An object o is kept at a depth H below the surface of a liquid of refractive index μ. What is apparent depth when the angle of vision at the surface is θ. a h=H/μ[μ cos θ/√μ2-sin2θ]3b h=H/μ[μ sin θ/√μ2-sin2θ]3 c h=μ/H[μ cos θ/√μ2-sin2θ]3 d none
The correct Answer is:Option
Correct Option :- d none Explanation :-Here it must be noted that the object when viewed from an angle θ not only shifts upwards by H-h but also laterally a-b with respect to its real position. If h is the apparent deptha= H tan i b = h tan θ a-b = H tan i – h tan θ a b H h are independent of small variation in θ & i 0 = H sec2 i di – h sec2 θ dθ di/dθ = [h sec2θ/H sec2i] ⇒ h =H sec2 i/sec2θdi/dθ = Hcos2θ/cos2idi/dθ 1 But as at the surface Snell’s Law μ sin i = 1 sin θ μ cos i di = cos θ dθ di/dθ = cos θ/μ cos i ...2 Substituting 2 in 1 we get h= H cos2θ/cos2idi/dθ = H cos2θ/cos2i cos θ/ μ cos i h = H[cos3θ/μ cos3i] 3 μ sin i = sin θ sin i = sinθ/μ √1-cos2 i = sinθ/μ 1-cos2 i =sin2θ/μ 1-sin θ/μ2 = cos2 i μ2- sin2θ/μ2= cos2 i √μ2- sin2θ/μ = cos i 4 Substituting cos i in 3 we get h= H cos3θ/μ cos3i =H/μ[μ3 cos3θ/μ2- sin2θ3/2] h = Hμ cos θ3/μμ2- sin2θ3/2
Related Solutions
If C is the critical angle for a medium and μ is its refractive index, then
View SolutionIf maximum and minimum values of for all real values of θ ≠ ( 2 n + 1 ) π 2 are ] , [ λ and μ respectively then
View SolutionAn object is placed at a distance of 10 cm (in a medium of μ = 1) from the pole of a spherical refracting surface bounding a medium of μ = 1.5. If the image formed is virtual and at a distance of 40 cm, then the spherical surface is –
View SolutionExplain how a body will move up in an incline with uniform velocity if the co.efficient of friction of the inclined plane is μ and the, angle of inclination of the plane to the horizontal is 'θ'
View SolutionFind minimum μ so that the blocks remain stationary.
View SolutionChoose the correctly'matched pair...(a)Lenz's law ⇒ ε = − (d ϕ B)/ d t (b)Faradays's law ⇒ M = μ r μ 0 n 1 n 2 A l (c)Lenz's law ⇒ B = μ 0 n I
View SolutionFind and if .
View SolutionA conducting circular loop is placed in a uniform magnetic field with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at . The induced emf in the loop when the radius is is:
(1.) 3.2 π μ V
(2.) 4.8 π μ V
(3.) 0.8 π μ V
(4.) 1.6 π μ V
View SolutionGive the number of ligand(s) which is//are non-classical ligand
.
View SolutionGive the number of ligand(s) which is//are non-classical ligand CO, NO, C_(2)H-(4),C_(3)H_(5) Θ , H^(Θ) .
View SolutionTwo point charges 4 μ and 8 μ are placed at a distance 1.5 m. Total number of points except infinity, where potential due to system of charges is zero?
View SolutionFind and if
View SolutionWhat is the maximum value of force, so that both the blocks will move together ? m1=m2=2kg ,μ=1/3

View SolutionClassify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid // base: a. overset(Θ)(O)H, b. F^(Θ), c. H^(o+), d. BCl_(3)
View SolutionClassify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid // base: a. overset(Θ)(O)H, b. F^(Θ), c. H^(o+), d. BCl_(3)
View SolutionClassify the following species into Lewis acids and Lewis bases and show how these act as Lewis acidbase:
a.
View Solution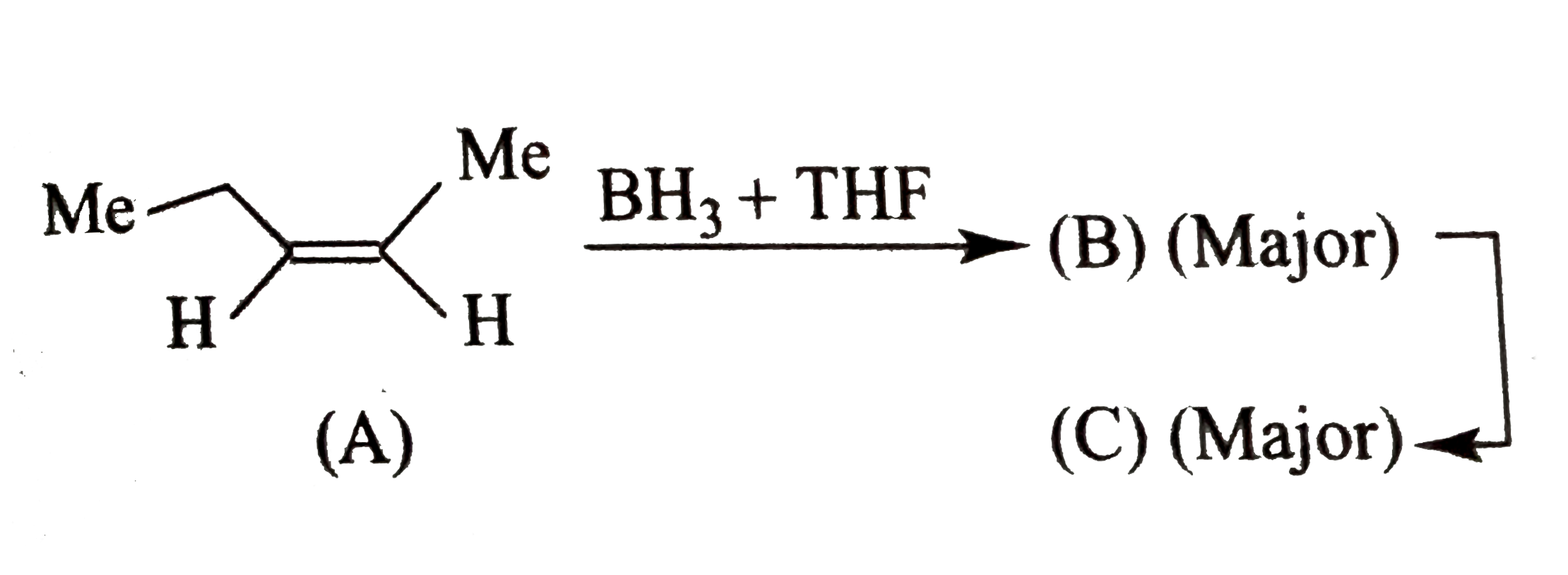
B and C are:
View SolutionCalculate for . Given:
, and are and
View SolutionCalculate K_(sp) for AgCI . Given: Delta_(f)H^(Θ) Ag^(o+) = 25.3 kcal mol^(-1) Delta_(f)H^(Θ) C1^(Θ) =- 40.0 kcal mol^(-1) Delta_(f)H^(Θ) AgC1=- 30.36 kcal mol^(-1) S^(Θ) Ag^(o+), S^(Θ) C1^(Θ) , and S^(Θ) AgC1 are 17.7, 13.2 and 23.0 cal mol^(-1)
View Solutiontwo charges 7 μ C and − 2 μ C placed at ( − 9 c m , 0 , 0 ) and (9 cm, 0,0) respectively. Suppose that the system of charges is now placed in an external field, E=A(1//r^2),A=9 times10^5C . What would the electrostatic energy of the configuration be?
View Solution