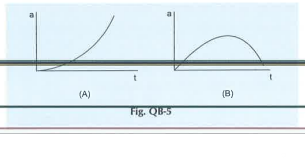
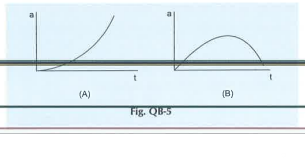
A particle is moving in a straight line whose acceleration versus time graph is given. Assume that initial velocity is in the direction of acceleration. Then which of the statement is correct between time t = 0 to t = t0.A Velocity first increases then decreases. B Velocity always increases from time zero to t0 C Displacement first increases then decreases. D Displacement always increases from time zero to t0
Correct option B Velocity always increases from time zero to t0D Displacement always increases from time zero to t0 Explanation:It is clear from the figure that acceleration does not change sign i.e. does not change in direction. Only the magnitude of acceleration first increases and then decreases. ∴ Velocity keeps on increasing.Hence displacement also keeps on increasing.
Related Solutions
Two particles, A and B, move along the same straight line. At t=0, there velocities are zero. Look at their acceleration-time graphs and say whether the statements given below are true or false
The velocity of B first increases and then decreases.
View SolutionA particle is moving in a straight line whose acceleration versus time graph is given. Assume that initial velocity is in the direction of acceleration. Then
which of the statement is correct between time to .
 .
.
View SolutionA particle is moving in a straight line whose acceleration versus time graph is given. Assume that initial velocity is in the direction of acceleration. Then
which of the statement is correct between time to .
 .
.
View SolutionTwo particles, A and B, move along the same straight line. At t=0, there velocities are zero. Look at their acceleration-time graphs and say whether the statements given below are true or false The velocity of each particle is continuously increasing.
View SolutionWhen an air bubble moves up from the bottom of a lake
a. Velocity decreases and becomes zero
b. acceleration increases and becomes zero
c. velocity increases and becomes constant
d. acceleration decreases and becomes zero
View SolutionWhen an air bubble moves up from the bottom of a lake
a) velocity decreases and becomes zero
b) acceleration increases and becomes zero
c) velocity increases and becomes constant
d) acceleration decreases and becomes zero
View SolutionTwo particles, A and B, move along the same straight line. At t=0, there velocities are zero. Look at their acceleration-time graphs and say whether the statements given below are true or false
The velocity of each particle is continuously decreasing.
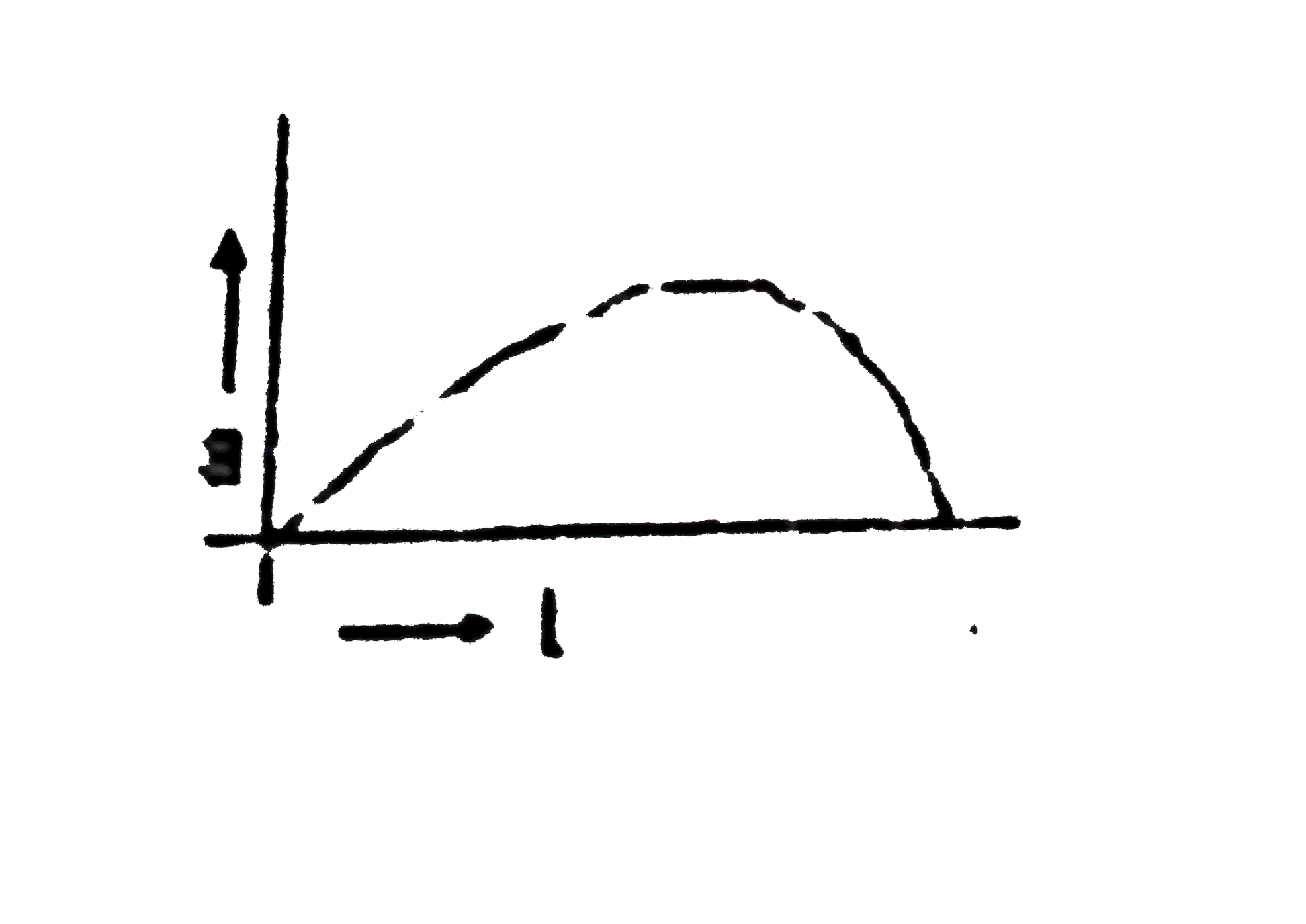
View SolutionThe acceleration of a particle is increasing linearly with time t as bt .The particle starts from the origin with an initial velocity v_(0) The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from origin with an initial velocity v_(0) . The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle is increasing linearly with time t as bt.The particle starts from origin with an initial velocity V_(0) .The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle increases linearly with time t by 6t. If the initial velocity of the particle is zero and the particle starts moving from the origin, then the distance covered by the particle in time t will be:
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t = t_1 and t = t_2.
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time

View SolutionThe acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
View SolutionThe acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
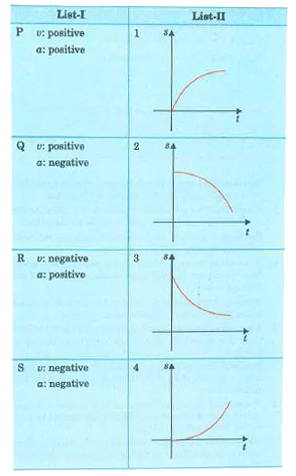
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity . The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity . The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v_0 . The distance travelled by the particle in time t will be
View SolutionThe acceleration of particle is increasing linearly with time t as bt . The particle starts from the origin with an initial velocity v_0 . The distance travelled by the particle in time t will be.
View Solution