A particle is moving along x-axis. Its position x varies with time t is shown in the graph. Points A B C D and E are also given in the graph. Here positive values of velocity and acceleration means they are towards +x direction and their negative values means that they are towards –x direction. Match the column–I according the correct results given in column–II. Centre of curvature of BD is below the graph but centre of curvature of AB and DE is above the graphCoulmn–IColumn–IIA From point A to Bp acceleration of the particle is positiveB From point B to Cq acceleration of the particle is negativeC From point C to Dr velocity of the particle is positive or zeroD From point D to Es speed is increasing
Correct option A – p r s ; B – q r ; C – q s ; D – p Explanation:v = slope of xt grapha = curvature of xt graph.
Related Solutions
The position time graph for a particle moving along X axis has been shown in the fig. At which of the indicated points the particle has (i) negative velocity but acceleration in positive X direction. (ii) positive velocity but acceleration in negative X direction. (iii) received a sharp blow (a large force for negligible interval of time)?
View SolutionA particle moves along -axis in positive direction. Its acceleration is given as , where denotes the - coordinate of particle, and are positive constants. For velocity position graph of particle to be of type as shown in figure, the value of speed of particle at should be
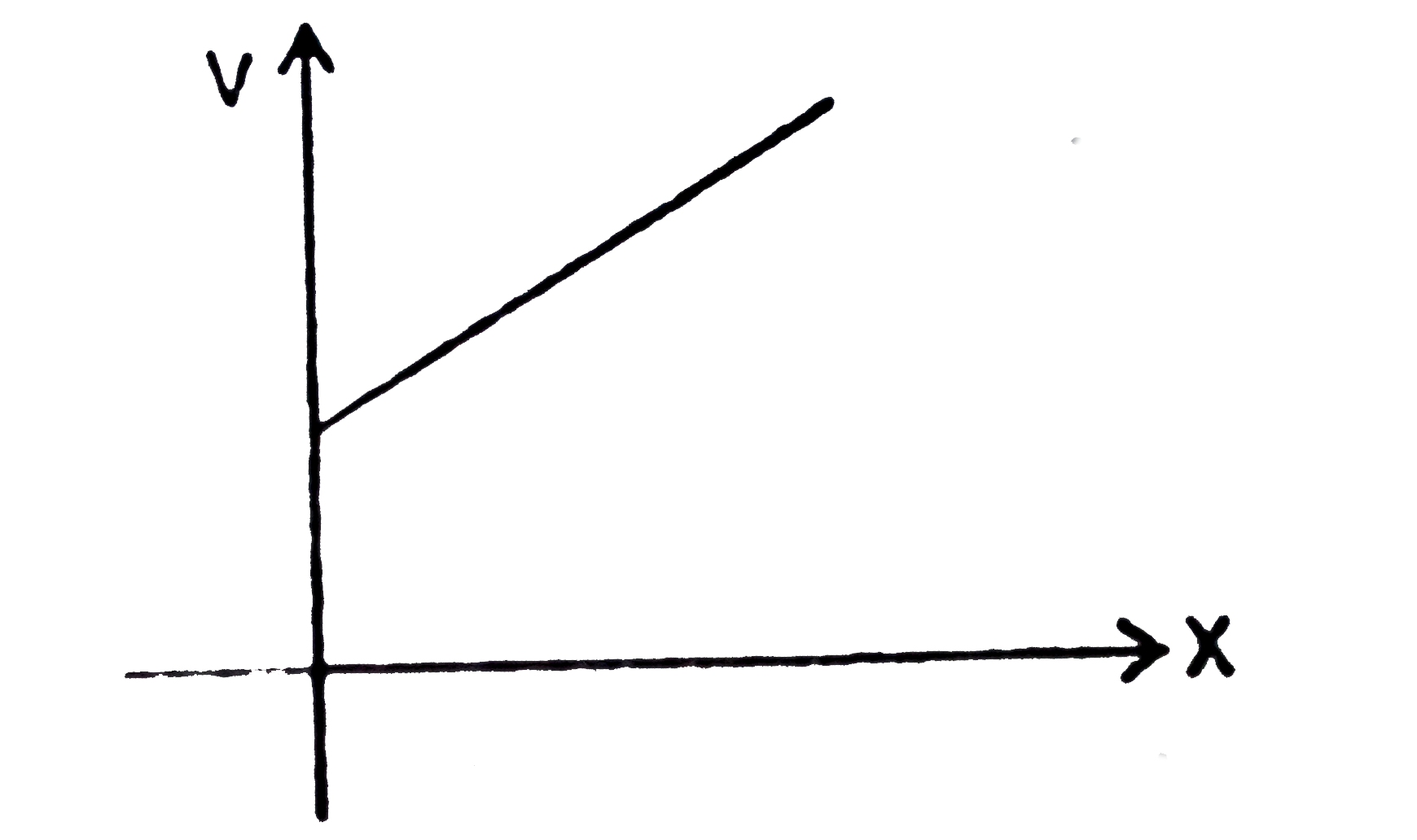
View SolutionA particle moves along -axis in positive direction. Its acceleration is given as , where denotes the - coordinate of particle, and are positive constants. For velocity position graph of particle to be of type as shown in figure,
the value of speed of particle at should be
View SolutionThe velocity of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
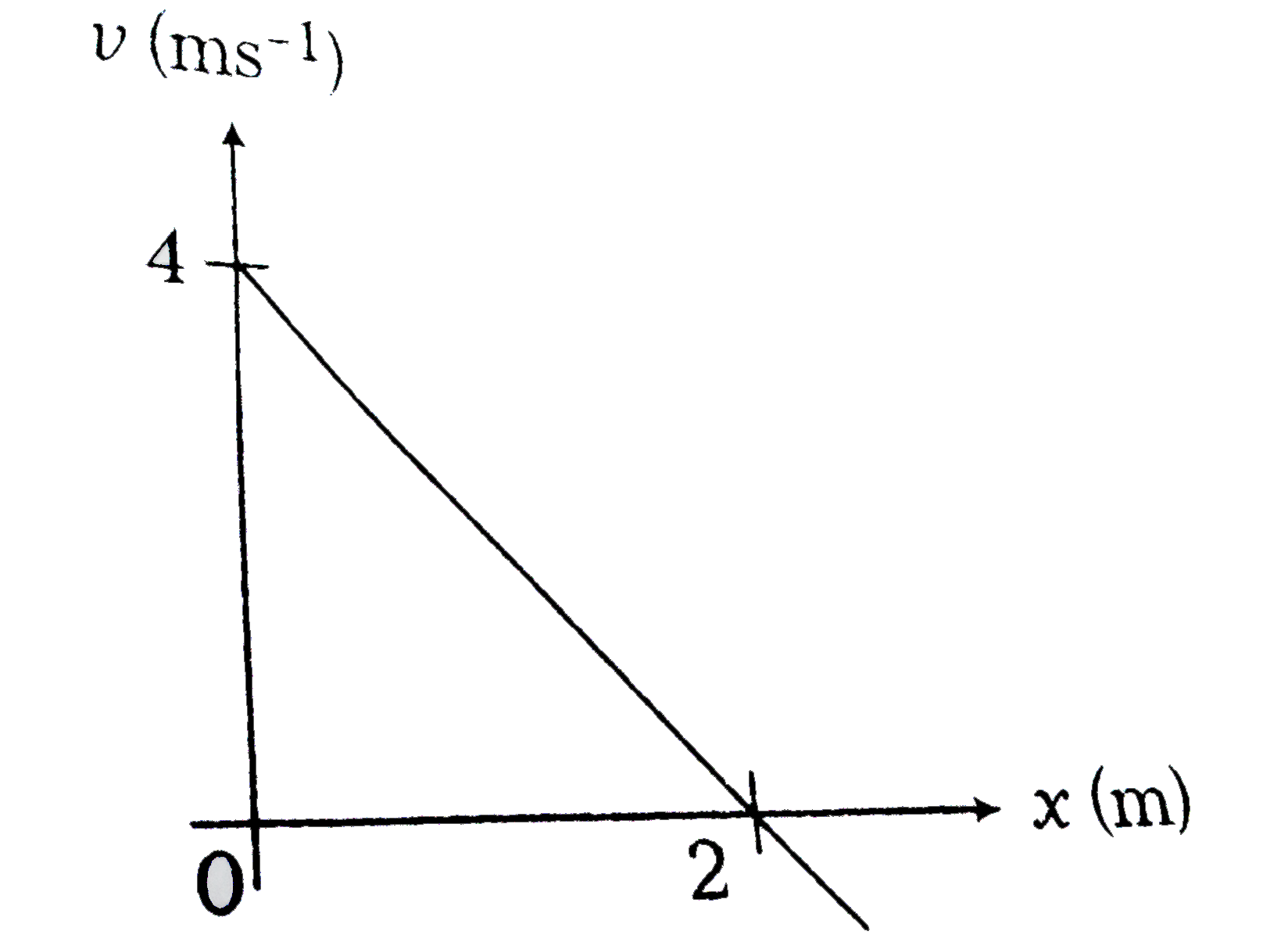
View SolutionThe velocity (upsilon) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment , and then heads back in the positive X-direction for .
What is the average velocity of the particle in the time interval to ?
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x = 4t + 2r^2, where x is in metres and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t = 1 s , and then heads back in the positive X-direction for t gt 1 s . What is the average velocity of the particle in the time interval t = 0 s to t = 1 s?
View SolutionA car is moving along a straight line. It's displacemetn (x)- time (t) grapg is shown in column II. Match the entries in column I with points on graph.
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
View Solution(a) If the position of a particle is given by , where is in meters and t is in seconds, when, if ever, is the particle's velocity v zero ? (b) When is its acceleration a zero ? For what time range ( positive or negative ) is a (c) negative and (d) positive ? (e) Graph , and a(t).
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x = 4t + 2r^2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t = 1 s , and then heads back in the positive X-direction for t gt 1 s . Find the instantaneous velocity of the particle at t = 2.5 s .
View SolutionThe velocity (v) - time (t) graph for a particle moving along x - axis is shown in the figure. The corresponding position (x) - time (t) is best represented by
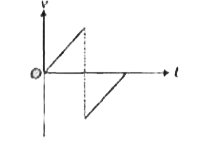
View SolutionThe velocity (v) - time (t) graph for a particle moving along x - axis is shown in the figure. The corresponding position (x) - time (t) is best represented by
View SolutionA particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation metre.
The velocity of the particle will vary with time according to the graph :-
View SolutionThe velocity-position graph of a particle moving in a straight line along x -axis is given below.Acceleration of particle at x=2m is
View SolutionDraw the acceleration-time graphs for the given velocity-time graphs of a particle moving along x-axis.

View SolutionDraw the acceleration-time graphs for the given velocity-time graphs of a particle moving along x-axis.

View Solution