Two men of masses m and m/2 starts climbing up on two mass less strings fixed at the ceiling with acceleration g and g/2 respectively. The ratio of tensions in the two strings will be :A 2 : 1 B 4 : 1 C 4 : 3 D 8 : 3
Correct option D 8 : 3Explanation:FBD of man of mass mFBD of man of mass m/2
Related Solutions
Two men of masses and starts climbing up on two masseless strings fixed at the ceiling with acceleration and respectively. The ratio of tensions in the two strings will be
View SolutionTwo men of masses and starts climbing up on two masseless strings fixed at the ceiling with acceleration and respectively. The ratio of tensions in the two strings will be
View SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is rho . The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator. Ratio of elongation in rod 1 to that of rod 2 will be
View SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is rho . The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator. Ratio of elongation in rod 1 to that of rod 2 will be
View Solutionद्रव्यमान m तथा m//2 एक दो व्यक्ति छत से जुडी हुई दो द्रव्यमानहीन डोरियों पर क्रमशः g तथा g/2 के त्वरणों के चढ़ना प्रारम्भ करते है। दोनों डोरियों में तनावों का अनुपात होगा -
View SolutionA mass of 1 kg is supended by a string. It is (i) lifted up with an acceleration 4.9 m//s^(2) (ii) lowered with an acceleration 4.9 m//s^(2) Then the ration of the tension in the string in the two cases is
View SolutionA pulley is attached to the ceiling of a lift going up. A string passes through the pulley with two particles attached at both ends. The masses of the particles are in the 2 : 1 ratio. If the acceleration of the particles is g/2, then the acceleration of the lift will be
View SolutionA mass of 1 kg attached to one end of a string is first lifted up with acceleration 4.9 m//s^(2) and then lowered with same acceleration. What is the ratio of tension in string in two cases.
View SolutionA block of mass si suspended by two strings angles and with the horizontal. Find the tensions in the strings.

View SolutionA mass of 2 kg tied to a string 1 m length is rotate in a verticle circle with a uniform speed of . The tension in the string will be 52 N, when the mass is at
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 )
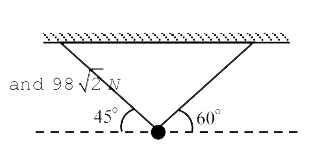
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m//s^(2) )
View SolutionA string is used to pull a block of mass m vertically up by a distance h at a constant acceleration (g)/(3) . The work done by the tension in the string is
View SolutionA string is used to pull a block of mass m vertically up by a distance h at a constant acceleration (g)/(3) . The work done by the tension in the string is
View SolutionIn fig. 16-47a, string 1 has a linear density of 3.00 g/m, and string 2 has a linear density of 5.00 g/m. They are under tension due to the hanging block of mass M= 800 g. Calculate the wave speed on (a) string 1 and (b) string 2 (Hint: When a string loops halfway around a pulley, it pulls on the pulley witii a net force that is twice the tension in the string) Next the block is divided into two blocks (with and the apparatus in tearranged as shown in fig. 16-47b. Find (c) such that the wave speeds in the two strings are equal.
View SolutionTwo bodies of masses 2 kg and 4 kg are connected at the two ends of a string of negligible mass that passes over an ideal pulley (i. e., of negligible mass and friction). Calculate (i) the acceleration of the system (ii) the tension in the string.
[Given: ]
View SolutionTwo boys of mass 10 kg and 8 kg are moving along a vertical rope, the first 2 m s^(-2) is climbing up with an acceleration of k while the other is 2 m s^(-1) is coming down with a uniform velocity of . Then the tension in the rope on a fixed base is - (g = 10 m s^(-2) take)
View SolutionTwo insects each of mass m moves with accelerations a_1 = a_2 = g//2 relative to the light inextensible string as shown in the figure. The ratio of tensions in the portions AB and BC of the string is :
View SolutionTwo masses =5kg, =10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
(a) g (b) (c) (d)
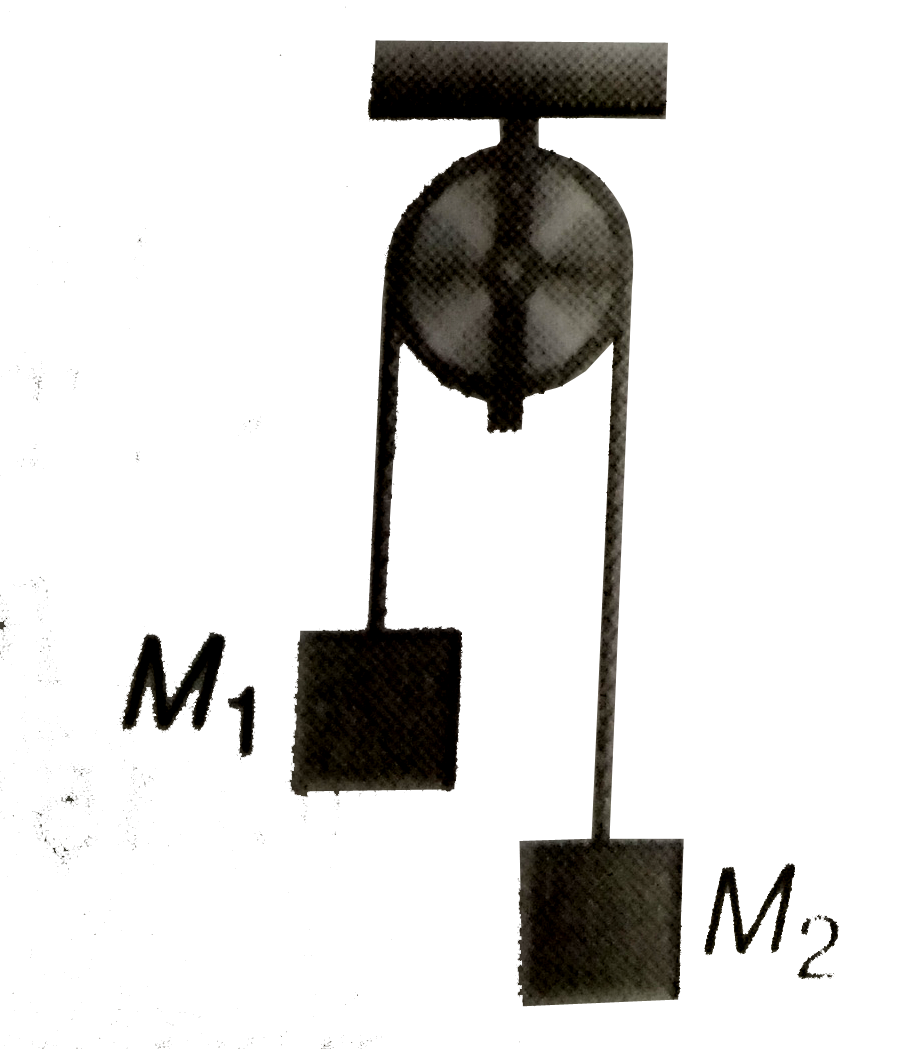
View Solution