Increasing the number of measurements of an experimental variable will- A increase the standard error of the sample B increase the mean of the sample C decrease the standard error of the sample D result in all of the above
The correct Answer is:Option
Correct Option :- C decrease the standard error of the sample
Related Solutions
Find out the correct answer out of the options given against each questions : In random sampling with replacement from a population with standard deviation if the sample size is equal to the population size, N, then the standard error of sample mean will be
View Solution............ Errors are related to the number and nature of the sample selected for the study. (samples, non-samples)
View SolutionIncreasing the number of measurement of an experimental variable will -
View SolutionWhich of the following errors is more serious and why ? (a) Sampling error. (b) Non-sampling error.
View SolutionA sample of 35 observations has the mean 80 and standard deviation as 4. A second sample of 65 observations from the same population has mean 70 and standard deviation 3. Then, the standard deviation of the combined sample is
View SolutionIf the first sample A of 100 items has the mean 15 and standard deviation 3 and second sample B has 150 items. If the combined mean and standard deviation of itmes of both the sample is 15.6 and then then standard deviation of items of sample B is
View SolutionThe mean life of a sample of 60 bulbs was 650 and the standard deviation was 8 h. A second sample of 80 bulbs has a mean life of 660 h and standard deviation 7h. Find the over all standard deviation.
View SolutionA sample of 25 variates has mean 40 and standand deviation 5 and a second sample of 35 variates has mean 45 and the standard deviation 2. Find the mean and standard deviation of the two samples of variates, taken together.
View Solutionतथा आकार के दो नमूनों का माध्य क्रमश: तथा और मानक विचलन क्रमश: तथा है। संयुक्त नमूने का माध्य के सापेक्ष मानक विचलन होगा
View SolutionSampling error is due to
View SolutionThe mean of two samples of size 50 and 100 respectively are 54.1 and 50.3 and the standard deviations are 8 and 7. Obtain the mean and standard deviation of the sample of size 150 obtained by combining the two samples.
View SolutionA sample of 35 observations has mean 80 men and standard deviation 4. A second sample of 65 observations has mean 70 and standard deviation =3. Find the combined mean and standard deviation.
View SolutionA simple of 25 variates has mean 40 and standard deviation 5 and a second sample of 35 variates has mean 45 and the standard deviation 2. Find the mean and standard deviation of the two samples of variates , taken together.
View SolutionAssertion : Rate of radioactivity cannot be increased or decreased by increasing or decreasing pressure or temperatur. Reason : Rate depends on the number of nuclei present in the radioactive sample.
View SolutionAssertion : Rate of radioactivity cannot be increased or decreased by increasing or decreasing pressure or temperatur. Reason : Rate depends on the number of nuclei present in the radioactive sample.
View SolutionA purchasing agent obtained samples of 60 watt bulbs from a standard company. He had the samples tested in his own laboratory for length of life with the following results:
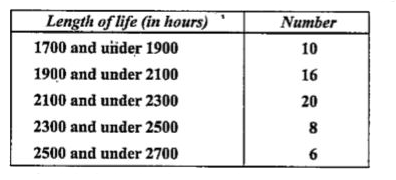
Calculate the standard deviation for these samples.
View SolutionA purchasing agent obtained samples of 60 watt bulbs from a standard company. He had the samples tested in his own laboratory for length of life with following results:

Find the standard deviation for these samples.
View SolutionDistinguish between (i) sampling, and (ii) non-sampling errors.
View SolutionThe mean life of a sample of 60 bulbs was 650 hours and the standard deviation was 8 hours. A second sample of 80 bulbs has mean life of 660 hours standard deviation 7 hours . Find the overall standard deviation.
View SolutionThe mean life of a sample of 60 bulbs was 650 h and the standard deviation was 8 h. A second sample of 80 bulbs has a mean life of 660 h and standard deviation 7 h. Find the overall standard deviation.
View Solution