A particle which is initially at rest at the origin is subjected to an acceleration with x- and y-components as shown. After time t = 5 sec. the particle has no acceleration.When is the particle at its farthest distance from the y-axis?A 3 sec. B 2 sec. C 4 sec. D 1 sec.
Correct option C 4 secExplanation:At t = 2 sec u = 10 × 2 = 20m/sAfter t = 2secv = u + at0 = 20 – 10tt = 2 sec.Hence at t = 4 sec. the particle is at its farthest distance from the y-axis. The particle is at farthest distance from y-axis at t ≥ 4. Hence the available correct choice is t = 4.
Related Solutions
A particle which is initially at rest at the origin, is subjection to an acceleration with and components as shown. After time , the particle has no acceleration.

When is the particle at its farthest distance from the axis ?
A. 3 sec.
B. 2 sec.
C. 4 sec.
D. 1 sec.
View SolutionA particle which is initially at rest at the origin, is subjection to an acceleration with and components as shown. After time , the particle has no acceleration.

When is the particle at its farthest distance from the axis ?
View SolutionA particle starts from rest on a straight path, Its acceleration is linearly varying with time, such that velocity of the particle at t=2 sec and t=4 sec is respectively. Find acceleration of the particle at t=i sec.
View SolutionThe acceleration of a particle, moving in a straight line, at time t is . If is the initial velocity of the particle then its velocity after 2 sec. is
View SolutionA particle is in SHM with time period 3 sec. Calculate the displacement of particle from mean position after t = 0.5 sec.
View SolutionA particle starts moving from rest with uniform acceleration. It travels a distance x in the first 2 sec and a distance y in the next 2 sec. Then
View SolutionA particle starts moving from rest with uniform acceleration. It travels a distance x in the first 2 sec and a distance y in the next 2 sec. Then
View SolutionA particle starts moving from rest with uniform acceleration. It travels a distance x in the first 2 sec and a distance y in the next 2 sec. Then
View SolutionA particle starts moving from rest with uniform acceleration. It travels a distance x in the first 2 sec and a distance y in the next 2 sec. Then
View SolutionA particle starts moving from rest with uniform acceleration. It travels a distance x in the first 2 sec and a distance y in the next 2 sec. Then
View SolutionA particle which is initially at rest at the origin, is subjection to an acceleration with and components as shown. After time , the particle has no acceleration.

What is the magnitude of velocity of the particle at seconds ?
View SolutionA particle which is initially at rest at the origin, is subjection to an acceleration with x- and y- components as shown. After time t=5 , the particle has no acceleration. What is the magnitude of velocity of the particle at t=2 seconds ?
View SolutionThe distance travelled in metres by a particle in second is given by . The speed of the particle after will be
View SolutionA particle starts moving from rest under a constant acceleration. It travels a distance x in the first 10 sec and distance y in the next 10 sec, then
View SolutionA particle describes a distance x m in t sec, given by x = 4+5t+63t^3 . Find the velocity of the particle at the end of 2 secs and the acceleration at the end of 3 secs
View SolutionA particle is moving on a circular path in xy-plane with centre at the origin. At t=0, it is (1,0). It has a constant angular velocity of (pi)/4 rad/s in clockwise direction {:("Column-I",,"Column-II"),("(A) has +ve x as well as +ve y-component.",,"(P) Acceleration at t=1 sec"),("(B) has -ve x as well as -ve y-component",,"(Q) Velocity at t=1 sec"),("(C) has -ve x but +ve y-component",,"(R) Position at t=1 sec"),("(D) has +ve x but -ve y-component",,"(S) Acceleration at t=3 sec"),(,,"(T) Velocity at t=3 sec"):}
View SolutionAcceleration of a particle moving in plane varies with time t as. .
Here a is in and t in sec. At time particle is at rest origin. Mass of the particles is . Find the net work done on the particle in first .
View SolutionFigure given here shows the variation of velocity of a particle with time.
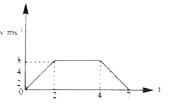
Find the following:
(i) Displacement during the time intervals.
(a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec
(ii) Accelerations at
(a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec.
(iii) Average acceleration
(a) between t = 0 to t = 4 sec.
(b) between t = 0 to t = 7 sec.
(iv) Average velocity during the motion.
View SolutionFigure given here shows the variation of velocity of a particle with time. Find the following: (i) Displacement during the time intervals. (a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec (ii) Accelerations at (a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec. (iii) Average acceleration (a) between t = 0 to t = 4 sec. (b) between t = 0 to t = 7 sec. (iv) Average velocity during the motion.
View SolutionThe motion of a particle along the x-axis is described by the following velocity function v(t)={:{((t^(3)+t^(2)+1),0 le t lt 3,"sec"),((2t+5),3 le t lt 5,"sec"),((t^(2)-6t),5 le t,"sec"):} where v is in m/sec and t is in second The chagne in acceleration of particle from t=3 sec to t=4 sec is
View Solution