Find the general solution by the method of variation of parameters.x2y − 4xy + 6y = x Be sure to express the equation in standard form before setting up variation of parameters.
First we have to solve the homogeneous equation 3.1 x2y − 4xy + 6y = 0. This is an Euler-Cauchy equation so we look for solutions of the form y = xm. The characteristic equation for m is mm − 1 − 4m + 6 = 0. Note mm − 1 − 4m + 6 = m2 − 5m + 6 = m − 2m − 3 so the roots are m = 2 and m = 3. Thus we have basic solutions y1 = x2 and y2 = x3 for the homogeneous equation 3.1. To solve the equation in the problem we put it in standard form by dividing both sides by x2. This gives usy -/xy + 6/x2y = 1/x.We look for a particular solution of this equation of the form y = uxy1x+ vxy2x. The equations for u and v are ux2 + vx3 = 0 2ux + 3vx2 = 1/x. If we multiply the top equation by −2 and the bottom equation by x the system becomes −2ux2 − 2vx3 = 0 2ux2 + 3vx3 = 1.Adding these equations gives vx3 = 1 so v = 1/x3. Substituting this is the first equation gives u = −1/x2. Easy integrations then giveu = 1/xv = − 1/2x2 Plugging into the formula y = uxy1x + vxy2x for our particular solution gives y = 1/xx2 − 1/2x2x3 = 1/2x. Adding on the general solution of the homogeneous equation we find y = 1/2x + C1x2 + C2x3 for the general solution of the inhomogeneous equation.
Related Solutions
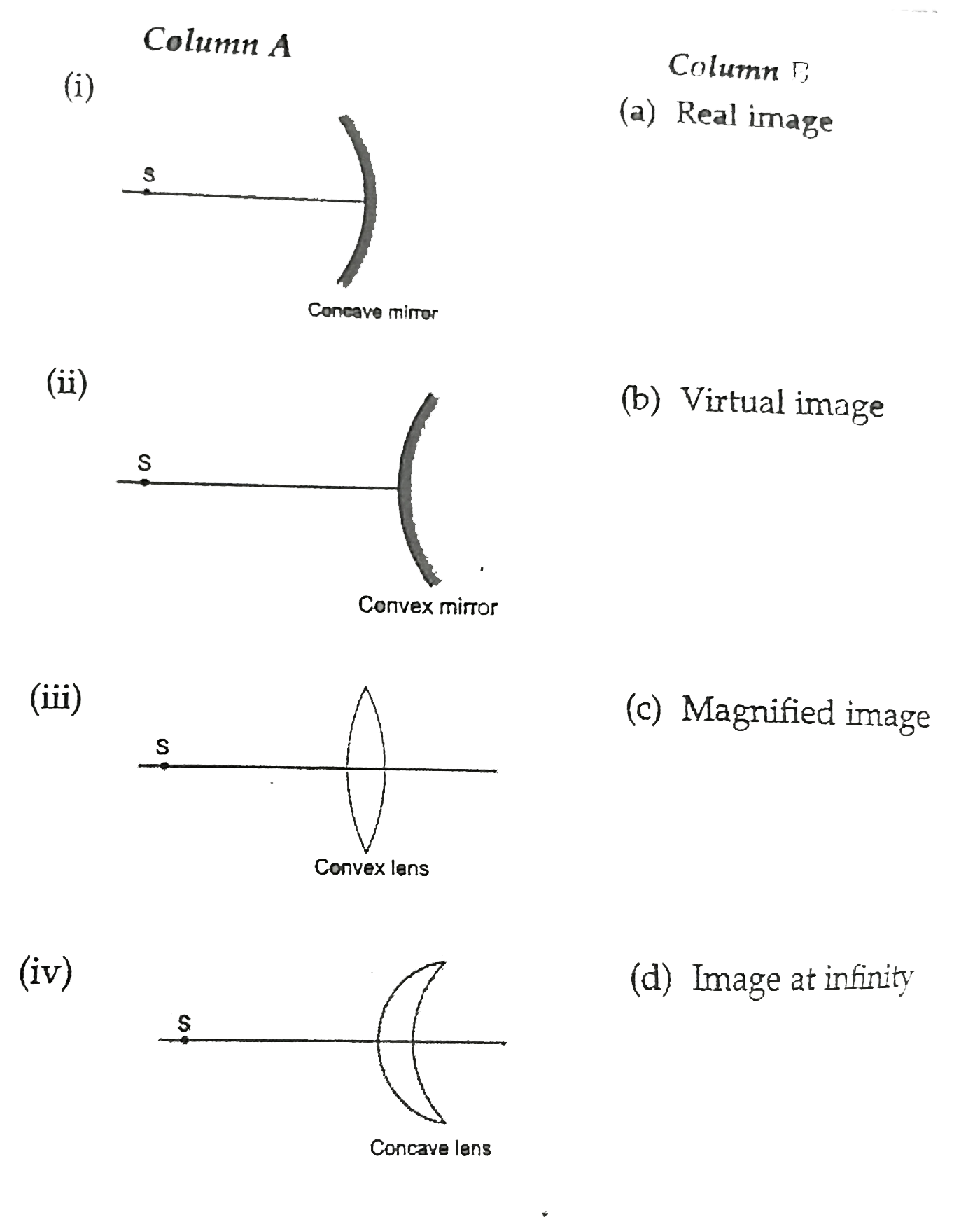
Column A gives a list of possible set of parameters measured in some experiments . The variations of the parameters in the form of graphs are shown in column B.
View SolutionColumn A gives a list of possible set of parameters measured in some experiments . The variations of the parameters in the form of graphs are shown in column B.
View SolutionThe coefficient of variation is defined as that is the standard deviation divided by the mean value. Find the coefficient of variation c.v. for each of the following set of observations.
2,3,4,2,5,7,8,9
View SolutionThe coefficient of variation is defined as that is the standard deviation divided by the mean value. Find the coefficient of variation c.v. for each of the following set of observations.
5,7,9,10,7,5,8,9,3
View SolutionThe coefficient of variation is defined as that is the standard deviation divided by the mean value. Find the coefficient of variation c.v. for each of the following set of observations.
3,3,3,4,4,4,5,5,5
View SolutionIf a variate x is expressed as a linear function of two variates u and v in the form x=au,bv, then mean overlinex of x is
View SolutionIf a variate X is expressed as a linear function of two variates U and V in the form X = aU + bV , then the mean barX of X is
View SolutionFind out standard deviation and coefficient of variation .
View SolutionA simple of 25 variates has mean 40 and standard deviation 5 and a second sample of 35 variates has mean 45 and the standard deviation 2. Find the mean and standard deviation of the two samples of variates , taken together.
View SolutionFind the constant of variation and the equation of variation in the following.
y varies inversely as x. If x = 3, y = 8
View Solutionx varies directly as y, when x = 5, y = 30. Find the constant of variation and equation of variation.
View Solutiony varies directly as square root of x. When x = 16, y = 24. Find the constant of variation and equation of variation.
View SolutionFind the constant of variation and the equation of variation in the following.
y varies directly as the square of x. When y = 128, x = 16.
View Solutiony varies directly as the square root of x. When x = 16, y = 24. Find the constant of variation and the equation of variation.
View SolutionIf a variate is expressed as a linear function of two variates and in the form , then mean of is
View SolutionIf a variate X is expressed as a linear function of two variates U and V in the form X=aU+bV then the mean bar(X) of X is
View SolutionIf a variate is expressed as a linear function of two variates and in the form , then mean of is
View SolutionIf a variate is expressed as a linear function of two variates and in the form , then mean of is
View SolutionWrite Arrhenius equation. Derive on expression for temperature variations.
View SolutionIf X is binomial variate with and variance 4. The parameters of the distribution are
View Solution