A ball is thrown from the roof of a building of height 44m with speed v0 at an angle θ below the horizontal. It lands 2 seconds later at a point 30m from the base of the building. If tanθ = X/10 then find the value of X. Take g = 10 m/s2
With the origin at the base
Related Solutions
A man runs across the roof of a tall building and jumps horizontally on to the (lower) roof of an adjacent building. If his speed is and the horizontal distance between the buildings is 10 m and the height difference between the roofs is 9 m, will he be able to land on the next building ? (take
View SolutionA boy playing on the roof of a high building throws a ball with a speed of at an angle of with the horizontal. How far from the throwing point will the ball be at the height of from the ground ?
View SolutionA man runs across the roof of a tall building and lumps horizontally on to the (lower) roof of an adjacent building. If his speed is 9 and the horizontal distance between the buildings is 10 m and the height difference between the roofs is 9 m, will he be able to land on the next building ? (take g = 10 ).
View Solutionएक गेंद को 44m ऊँची मीनार की छत से चाल से क्षैतिज के नीचे कोण पर फेंका जाता है। यह मीनार के आधार से 30 म दुरी पर स्थित एक बिन्दु पर 2 सैकण्ड में पहुँचती है यह तो X का मान ज्ञात करों
View SolutionA ball is dropped from a building. It takes 4s to reach the ground. The height of the building is (use g = 10 m//s^(2) )
View SolutionA man runs across the roof of a tall building and jumps horizontally on to the (lower) roof of an adjacent building. If his speed in and the horizontal distance between the buildings is 10 m and the height difference between the roof is 9m, will he is able to land on the next buildings? (take )
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle 30 ^@ with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground? (g = 10 m//s ^ 2 )
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle 30 ^@ with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground? (g = 10 m//s ^ 2 )
View SolutionA boy playing on the roof of a high building throws a ball with a speed of at an angle of with the horizontal. How far from the throwing point will the ball be at the height of from the ground ?
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle of 30° with the horizontal. How far from the throwing point will be ball be at the height of 10 m from the ground ?
View SolutionA boy playing on the roof of a high building throws a ball with a speed of at an angle of with the horizontal. How far from the throwing point will the ball be at the height of from the ground ?
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m//s at an angle of 30(@) with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground ? [ g = 10m//s^(2) , sin 30^(@) = (1)/(2) , cos 30^(@) = (sqrt(3))/(2)]
View Solutionएक गेंद को भवन की छत से गिराने पर गेंद को जमीन पर पहुँचने में 3 सेकण्ड लगते हैं। गेंद के पृथ्वी की ओर त्वरण 10 मी/से है, तो भवन की ऊँचाई है
View Solutionएक ऊँची ईमारत की छत से किसी पत्थर को क्षैतिज के साथ कौन बनाते हुए फेंका जाता है यह तीन सैकण्ड बाद धरातल पर पहुँचता है यदि फेंकने के दो सैकण्ड बाद यह छत के स्तर पर था तो ईमारत की ऊँचाई है
View SolutionA man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building?
View SolutionA ball is thrown from the top of a building with a velocity of 10 m/s and returns with a velocity of 30 m/s to the ground. Find the height of the building.
View SolutionWhen a ball is dropped from the roof of a building, it takes 3 seconds for the ball to reach the ground. acceleration of the ball towards the earth 10 "मी"//"से"^(2) then the height of the building is
View Solutionएक आदमी 10 मी. ऊँचे घर की छत से एक भवन के शीर्ष का उन्नयन कोण और आधार का अवनमन कोण देखता है । भवन की ऊँचाई और इसकी घर से दूरी ज्ञात कीजिए।
View SolutionA window in a building is at a height of 10 m from the ground. The angle of depression of a point P on the ground from the window is . The angle of elevation of the top of the building from the point P is . Find the height of the building.
View SolutionA ball is thrown downwards with a speed of , from the top of a building high and simultaneously another ball is thrown vertically upwards with a speed of from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
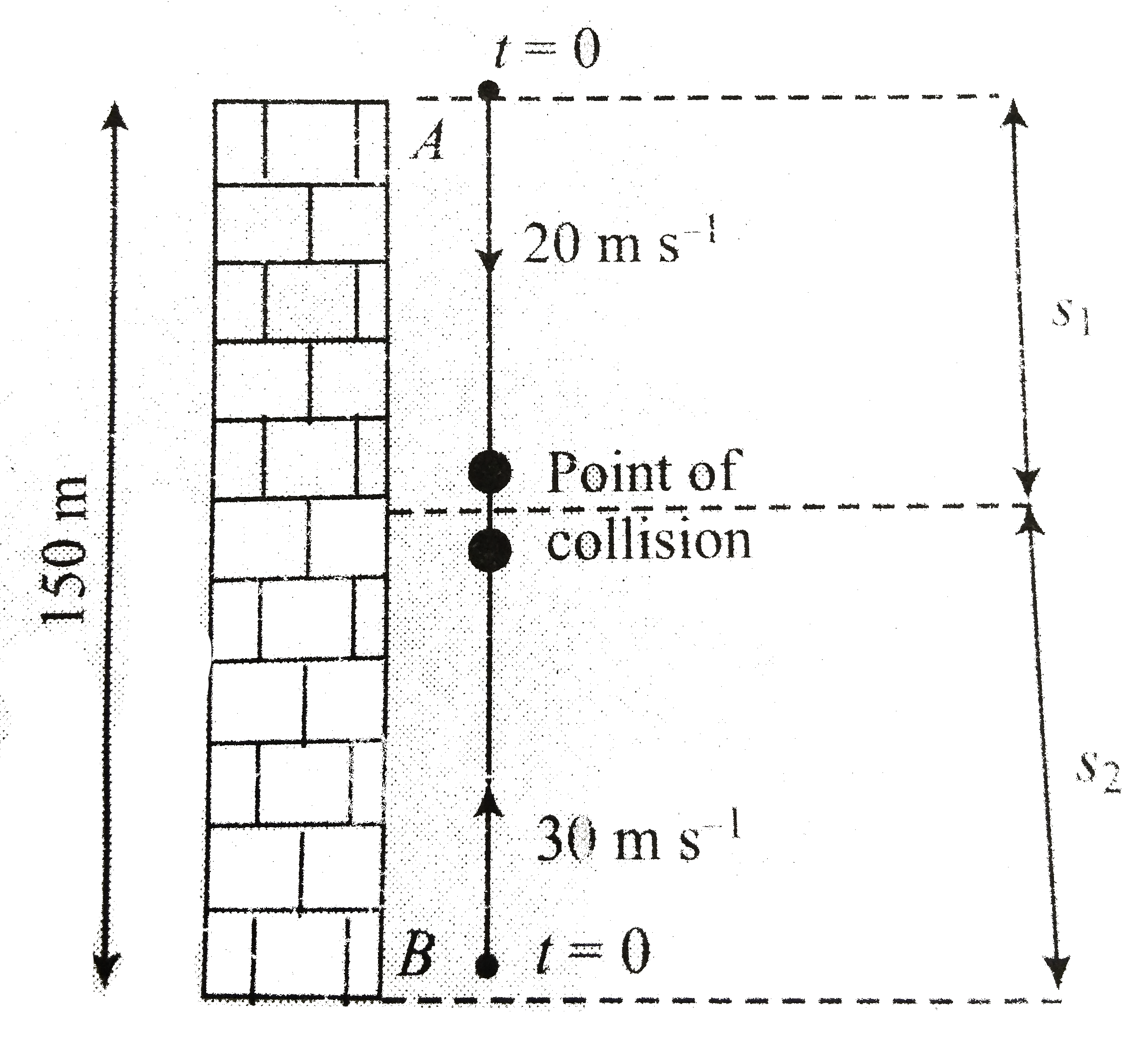 .
.
View Solution