I-V characteristics of a copper wire of length L and area of cross-section A is shown in figure. The slope of the curve becomes1 More if the experiment is performed at higher temperature 2 More if a wire of steel of same dimension is used3 More if the length of the wire is increased 4 Less if the length of the wire is increased
Correct option 4 Less if the length of the wire is increasedExplanation: Slope of V-i curve =R=ρl/A. But in given curve axis of i and V are interchanged. So slope of given curve =1/R=A/ρl i.e. with the increase in length of the wire. Slope of the curve will decrease.
Related Solutions
I- V characteristic of a copper wire of length of L and area of cross - section A is shown in figure . The slope of the curve becomes .
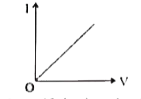
View SolutionI-V characteristic of a copper wire of length L and area of cross-section A is shown in the figure. The slope of the curve becomes
View Solutionl-V characteristic of a copper wire of length Land area of cross-section A is shown in figure. The slope of the curve becomes
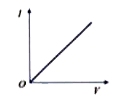
View Solutioncharacteristics of a copper wire of length and area fo cross-section is shown in Fig. The slope of the curve becomes
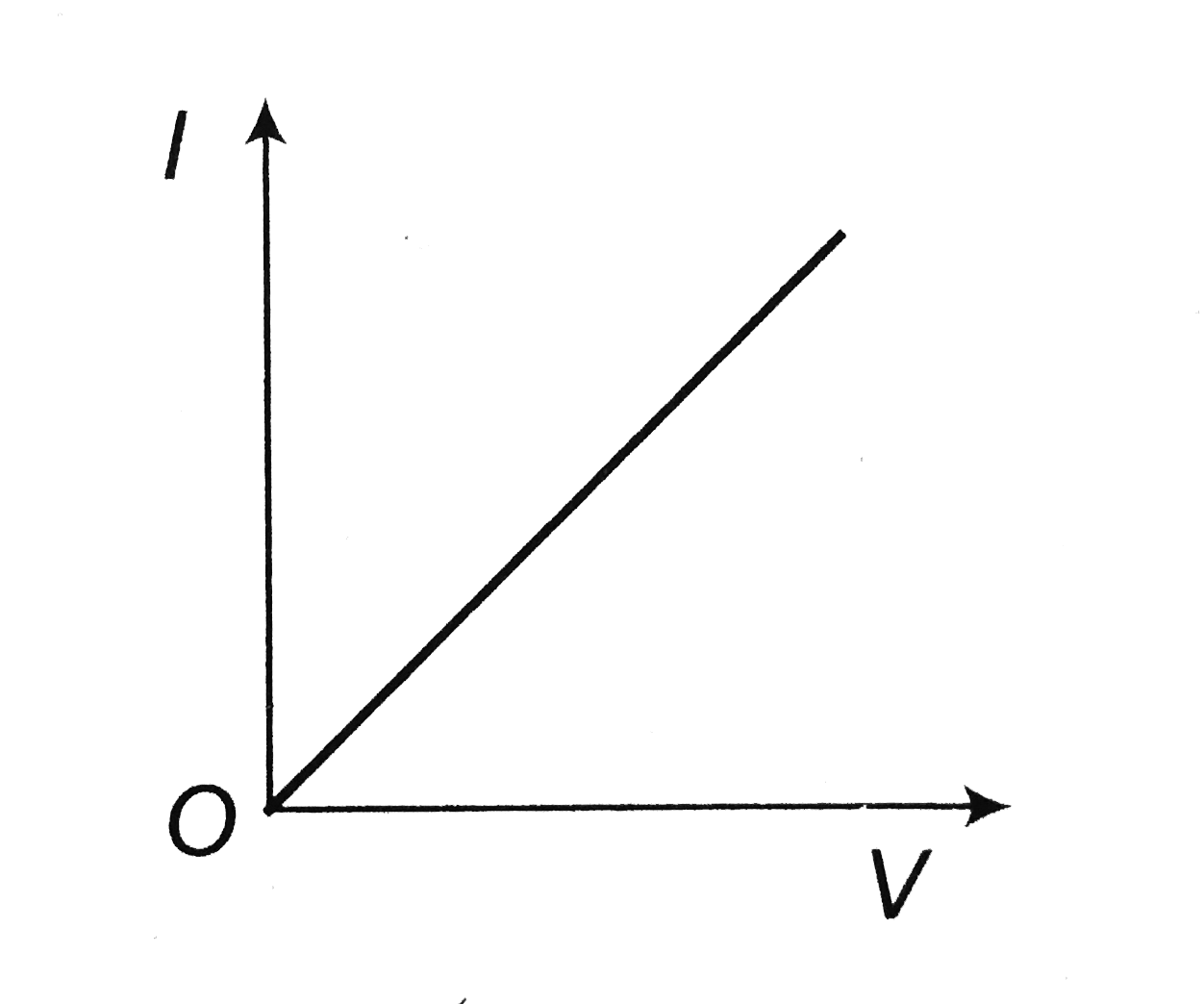
View SolutionI-V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
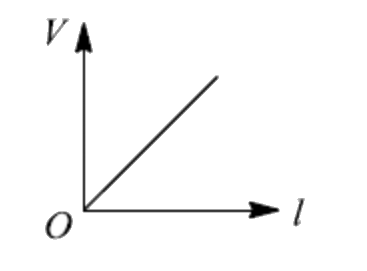
View SolutionThe V – I graph for a wire of copper of length L and cross -section area A is shown in the figure below . The slope of the graph will be
View SolutionThe V – I graph for a wire of copper of length L and cross -section area A is shown in the figure below . The slope of the graph will be
View SolutionThe V- I graph for a copper wire of length L and cross-sectional area A is shown in the figure below. Slope of the article:
View SolutionThe V – I graph for a wire of copper of length L and cross -section area A is shown in the figure below . The slope of the graph will be
View SolutionThe ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
View SolutionAssertion : Resitivity of a wire of length 2L is double that of half the wire of length L. Reason : Increasing the length of a wire decrease its cross-sectional area.
View Solutionदो तार समान पदार्थ के बने हैं और दोनों के आयतन भी समान हैं । पहले तार के अनुप्रस्थ काट का क्षेत्रफल A तथा दूसरे तार के अनुप्रस्थ काट का क्षेत्रफल 3A है । यदि बल F लगाकर पहले तार की लंबाई में की वृद्धि की जाती है, तो दूसरे तार की लंबाई में इतनी ही वृद्धि करने के लिए कितने बल की आवश्यकता होगी -
View SolutionI-V characteristic of a copper of length L and area of cross-section A is shown in the figure. The slope of the curve becomes

View SolutionA copper wire and a steel wire of the same length and same cross-section are joined end to end to form a composite wire. The composite wire is hung form a rigid support and a load is suspended form the other end. If the increses in length of the composite wire is . then the increases in lenghts of steel and copper wires are
View SolutionThe radius of a copper wire is twice that of a steel wire. One end of the copper wire is joined with one end of the steel wire and the same tensile force is applied on them . If the length of the copper wire increases by 1% , what will be the percentage increase in the length of the steel wire? Given Young's modulus of steel is twice that of copper.
View SolutionA composite wire is prepared by joining a tungsten wire and steel wire Both the wires are of the same length and same area of cross section. If this composite wire is suspended to a rigid support and a force is applied to its free end, it gets extended by 3.25 mm. Calculate the increase in length of tungsten wire and steel wire separately.
View SolutionA composite wire is prepared by joining a tungsten wire and steel wire end to end. Both the wires are of the same length and the same area of cross section. If this composite wire is suspended to a rigid support and a force is applied to its free end, it gets extended by 3.25mm. Calculate the increase in length of tungsten wire and steel wire separately
View SolutionTwo wires are made of the same material and have the same volume. However wire 1 has cross-section area A and wire 2 has cross-section area 3A. If length of wire 1 increased by
View Solutionदो तार समान पदार्थ के बने हैं और दोनों के आयतन भी समान हैं। पहले तार के अनुप्रस्थ-काट का क्षेत्रफल A और दूसरे तार के अनुप्रस्थ-काट का क्षेत्रफल 3A है। यदि बल F लगाकर पहले तार की लम्बाई में की वृद्धि की जाती है, तो दूसरे तार की लम्बाई में भी इतनी ही वृद्धि करने के लिए कितने बल की आवश्यकता होगी?
View SolutionTwo wires are made of the same material and both have the same volume. The area of cross-section of the first wire is A and the area of cross-section of the second wire is 3A. If the length of the first wire by applying a force F Deltal is increased, then how much force will be required to increase the length of the second wire by the same amount?
View Solution