A loop carrying current I has the shape of a regular polygon of n sides. If R is the distance from the centre to any vertex then the magnitude of the magnetic induction vector B G at the centre of the loop is –
Correct :- Explanation :-
Related Solutions
A loop carrying current I has the shape of a regular polygon of n sides. If R is the distance from the centre to any vertex, then the magnitude of the magnetic induction vector at the centre of the loop is –
View SolutionA wire bent in the shape of a regular n-polygonal loop carries a steady current I. Let be the perpendicular distance of a given segment and R be the distance of vertex both from the centre of the loop. The magnitude of the magnetic field at the centre of the loop is given by -
View SolutionEach side of a hexagonal loop of a metal wire is a. The loop carries a current I. Find the magnitude of the magnetic field at the centre of the loop
View SolutionA square loop of side a carris a current . The magnetic field at the centre of the loop is
View SolutionA square loop of side a carris a current I . The magnetic field at the centre of the loop is
View SolutionA current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when is (R is the radius of its circumcircle)
View SolutionA current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when ntooo is (R is the radius of its circumcircle)
View SolutionMagnetic induction produced at the centre of a circular loop carrying current is B . The magnetic moment of the loop of radius R is
View SolutionA hexagonal loop of a metallic wire is of each side a and carries a current I . Find the magnitude of magnetic field at the centre of the loop.
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionA square loop of side carries a current . Calculate magnetic induction at point P, lying on the axis of loop and at a distance from the centre of loop.
View Solution(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.
View SolutionA square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
View SolutionMagnetic field induction at the centre of a square loop of side 'a' carrying current I as shown in figure is
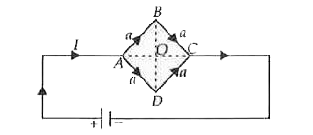
View SolutionMagnetic field induction at the centre O of a square loop of side a carrying current I as shown in figure.
View SolutionA regular polygon of 'n sides is formed by bending a wire of length which carries a current i. Find the magnetic field at the centre of the polygon?
View SolutionA circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field (a) at the centre of the loop and (b) at a distance of 9.7 cm from the centre of the loop but on the axis.
View SolutionMagnetic induction produced at the centre of a circular loop carrying current is B . The magnetic moment of the loop of radius R is (Me = permeability of tree space)
View SolutionWhat is the magnetic moment of a current carrying thin circular loop if the radius of the loop is equal to R and the magnetic induction at its centre is equal to B ?
View Solution