Find L[1/√t]
Given L[1/√t] = L[t-1/2]
Related Solutions
The stability of +1 oxidation state in aqueous solution is in the order- A l I n > T l T l > In > G a > A l A l > T l > G a > In T l > A l > G a > In
View SolutionIf then find .
View SolutionDimensions of are
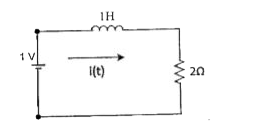
View SolutionFor the R-L circuit shown in the figure, the input voltage . Find the current i(t) for sec.
View SolutionIf then find .
View SolutionThe time T of oscillation of a simple pendulum of length l is given by .
Find the percentage error in T corresponding to
(i) on increase of in the value of l.
(ii) decrease of in the value of l.
View SolutionThe graph shows the variation of l nR v//s (1)/(T^(2)) , where R is resistance and T is temperature. Then find R as function T .
View SolutionThe graph shows the variation of , where is resistance and is temperature. Then find as function .
_2019_CBT5_E01_037_Q01.png)
View SolutionName the quantites represented by the dimensional formula [M^1 L^2 T^(-1)] , [M^1 L^2 T^(-2)][M^1 L^(-3) T^0].
View Solution
View Solution
View Solutionare the dimensions of
View Solutionare the dimensions of
View Solutionare the dimensions of
View Solution[L^(-1)M^(1)T^(-2)] are the dimensions of
View SolutionDimensions are related to .............
View SolutionMatch the following: {:(," ""Column-I",," ""Column-II"),((a),F = A sin(B t) + (1)/(C ln (Dx)) "For above equation to be dimensionally correct",(p),[A] = [M^(1)L^(1)T^(-1)]","[B] = [M^(0)L^(0)T^(-1)]","[C] = [M^(0)L^(0)T^(-1)]),((b) ,"Pressure" = P + (1)/(2)rhov^(2) + gX ,(q),[A] = [M^(0)L^(1)T^(-1)]"," [B] = [M^(0)L^(0)T^(-1)]","[C] = [M^(0)L^(0)T^(-1)]","),((c),X = At+(v)/(B ln(Cr)),(r),[A] = [M^(1)L^(1)T^(-2)]","[B] = [M^(0)L^(0)T^(-1)]","[C] = [M^(-1)L^(0)T^(1)]),(,,(s),"Dimensionally incorrect""):} (Where F = force, P = pressure, rho = density, t = time, v = velocity, a = acceleration, X = displacement)
View SolutionThe time T of of oscillation of a simple pendulum of length l is given by . Find the percentage error in T, corresponding to an error of in the value of l.
View SolutionThe time t of a complete oscillation of a simple pendulum of length l is given by where g is gravitational constant. Find the approximate percentage of error in t when the percentage of error in l is 1%.
View SolutionThe time period T of oscillation of a simple pendulum of length l is given by T=2pi. sqrt((l)/(g)) . Find the percentage error in T corresponding to 2% in the value of l.
View Solution