Two solid spheres A and B of equal volumes but of different densities dA and dB are connected by a string. They are fully immersed in a fluid of density dF. They get arranged into the equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only ifA dA dF C dA> dF D dA + dB= 2dF
The correct Answer is:Option
Correct Option A B DExplanation:Equilibrium of B T + VdFg = VdBg ….iiAdding eqns. i and ii we get2df = dA + dB∴ Option d is correct. From Eq. i we can see thatdF > dA as T>0∴ Option a is correct. From equation ii we can see that dB > dF∴ Option b is correct. ∴ Correct options are a b and d.
Related Solutions
Two solid spheres A and B of equal volumes but of different densities are connected by a string. They are fully immersed in a fluid of density . They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
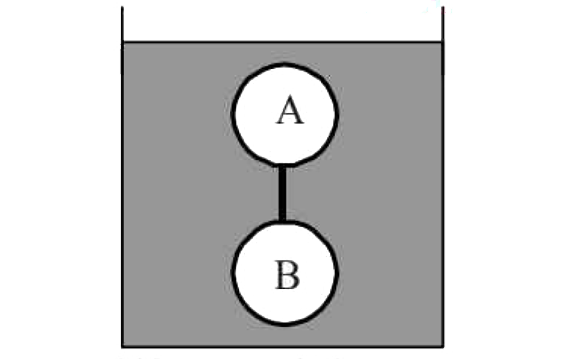
View SolutionTwo solid spheres A and B of equal volumes but of different densities are connected by a string. They are fully immersed in a fluid of density . They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if

View SolutionTwo solid spheres A and B of same volume but different densities dA and MB are connected by a thread. It is completely immersed in a liquid of density of K. Both of them are in equilibrium with the taut thread as shown in the picture. This provision is possible if -
View SolutionFor the reaction the rate is equal to
View SolutionIf then the value of at (2,2) is :
View SolutionIn the given figure DA _|_ OP and DB _|_OQ and /_ADB = 170^@ find /_AOB .
View SolutionProve that is equal to OA+OB+OC.
View SolutionProve that is equal to OA+OB+OC.
View SolutionIn a triangle are points on respectivley, such that Let be the point of intersection of Find using the vector method.
View SolutionIn a triangle A B C ,Da n dE are points on B Ca n dA C , respectivley, such that B D=2D Ca n dA E=3E Cdot Let P be the point of intersection of A Da n dB Edot Find B P//P E using the vector method.
View SolutionIn a triangle are points on respectivley, such that Let be the point of intersection of Find using the vector method.
View SolutionIn a triangle are points on respectivley, such that Let be the point of intersection of Find using the vector method.
View SolutionIf A,B,C,D And E five is a planar vector DA+DB+DC+AE+BE+CE The value of
View SolutionIn the given figure, we have C is the mid-point of AB and DA = DB.
Prove that : .
View SolutionLet ABC be a triangle, right-angled at B and D be the midpoint of AC. Show that DA = DB = DC.
View SolutionIf are five coplanar points, then the value of is equal to
View Solutionif A,B,C,D and E are five coplanar points, then is equal to
View Solutionif A,B,C,D and E are five coplanar points, then is equal to
View Solutionif A,B,C,D and E are five coplanar points, then is equal to
View SolutionIf A,B,C,D and E are five coplanar points,( then the value of )/(DA)+bar(DB)+bar(DC)+bar(AE)+bar(BE)+bar(CE) is equal to
View Solution