The total work done on a particle is equal to the change in its kinetic energy a always b only if the forces acting on it are conservative c only if gravitational force alone acts on it d only if elastic force alone acts on it.
a alwaysExplanation: Whatever be the force the work done on the particle by the resultant force is always equal to the change in its K.E. Either increase or decrease.
Related Solutions
[" Question "7],[" The total work done on a particle is equal to the change in its kinetic energy "],[" o always "],[" only if the forces acting on the body are conservative "],[" o only in the inertial frame "],[" only if no external force is acting "]
View SolutionSTATEMENT-1: Work done by the net force acting on a particle is equal to the change in its kinetic energy.
STATEMENT-2: Change in potential energy is always equal to the work done by external forces.
STATEMENT-3: Work energy theorem is not applicable, if the work is done by the non-conservative forces
View SolutionSTATEMENT-1: Work done by the net force acting on a particle is equal to the change in its kinetic energy. STATEMENT-2: Change in potential energy is always equal to the work done by external forces. STATEMENT-3: Work energy theorem is not applicable, if the work is done by the non-conservative forces
View SolutionStatements: The trajectory of a particle depends only on the force acting on it. Reason: The velocity and position of the particle depends only on the force acting on it.
View SolutionIf only the force of gravitational force is acting on an object, what is the initial velocity of that object?
View SolutionStarting at rest , object is acted upon by only one force as indicated in figure. Then the total work done by the force is
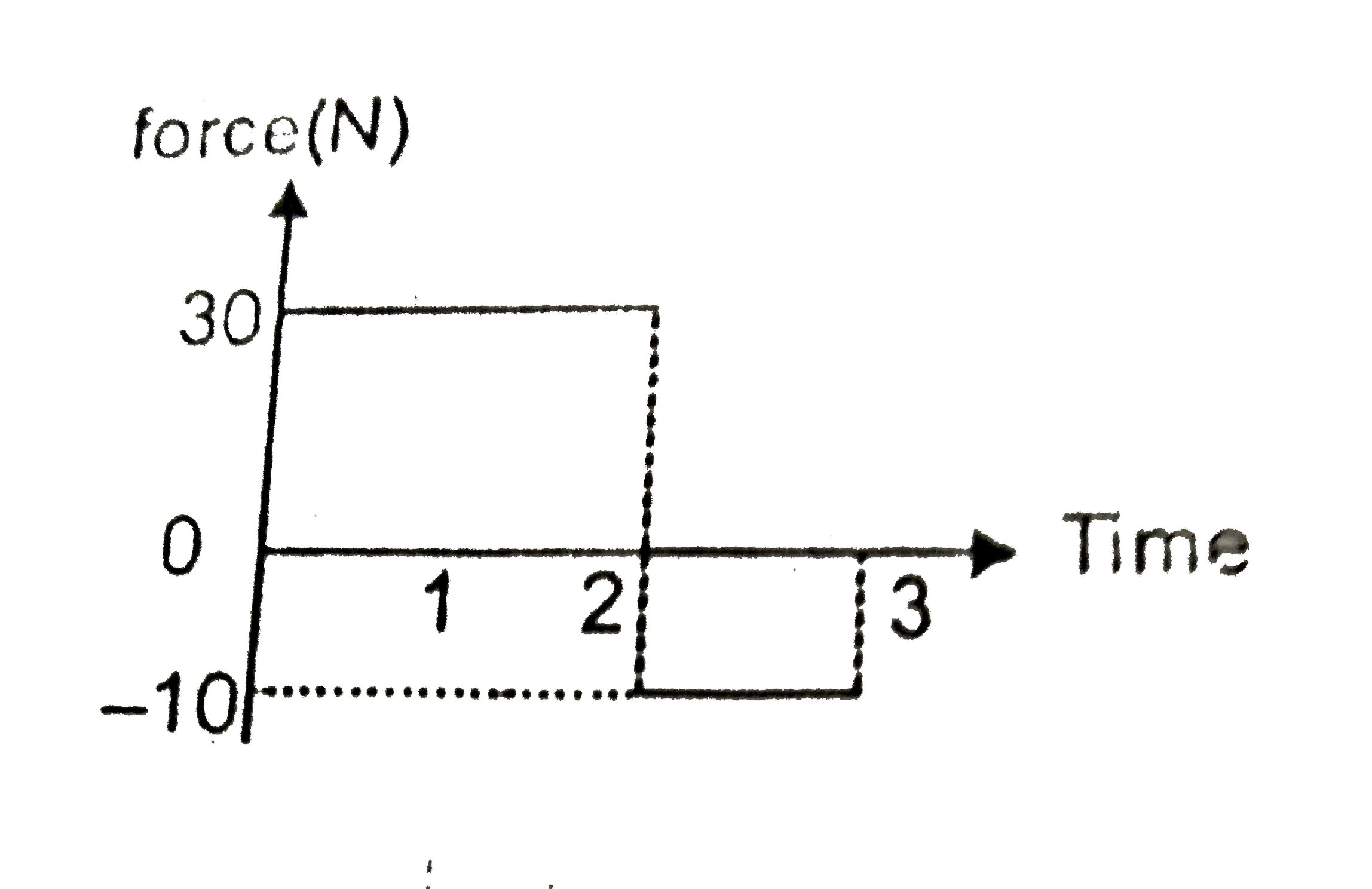
View SolutionStarting at rest , object is acted upon by only one force as indicated in figure. Then the total work done by the force is

View SolutionA : The change in kinetic energy of a particle is equal to the work done on it by the net force. R : The work-energy theorem can be used only in conservative field.
View SolutionA : The change in kinetic energy of a particle is equal to the work done on it by the net force. R : The work-energy theorem can be used only in conservative field.
View SolutionThe only force acting on the projectile is
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a . The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions. Force acting on particle C , due to particle A and B
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a . The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions. Force acting on particle C , due to particle A and B
View Solution(A) : The change in kinetic energy of a particle is equal to the work done on it by the net force.
(R ) : Change in kinetic energy of particle is equal to the work done only in case of a system of one particle.
View SolutionStatement The work done by all forces on a system equals to the change in kinetic energy of that system . This statement is true even if nonconservative forces act on the system.
Statement The total work done by internal forces may be positive.
View SolutionStatement -1: The work done by all forces on a system equals to the change in kinetic energy of that system . This statement is true even if nonconservative forces act on the system. Statement -2: The total work done by internal forces may be positive.
View SolutionA particle is acted upon by only a conservative force F=(7hat(i)-6hat(j)) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
View SolutionA particle is acted upon by only a conservative force F=(7hat(i)-6hat(j)) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
View SolutionA : If net force acting-on a system is zero, then work done on the system may be nonzero.
R : Internal forces acting on a system can increase its kinetic energy.
View SolutionA : If net force acting-on a system is zero, then work done on the system may be nonzero. R : Internal forces acting on a system can increase its kinetic energy.
View SolutionStatements: The change in kinetic energy of a particle is equal to the work done by the resultant force on it. Reason: The change in kinetic energy of a particle is equivalent to the work done for a particle body only.
View Solution