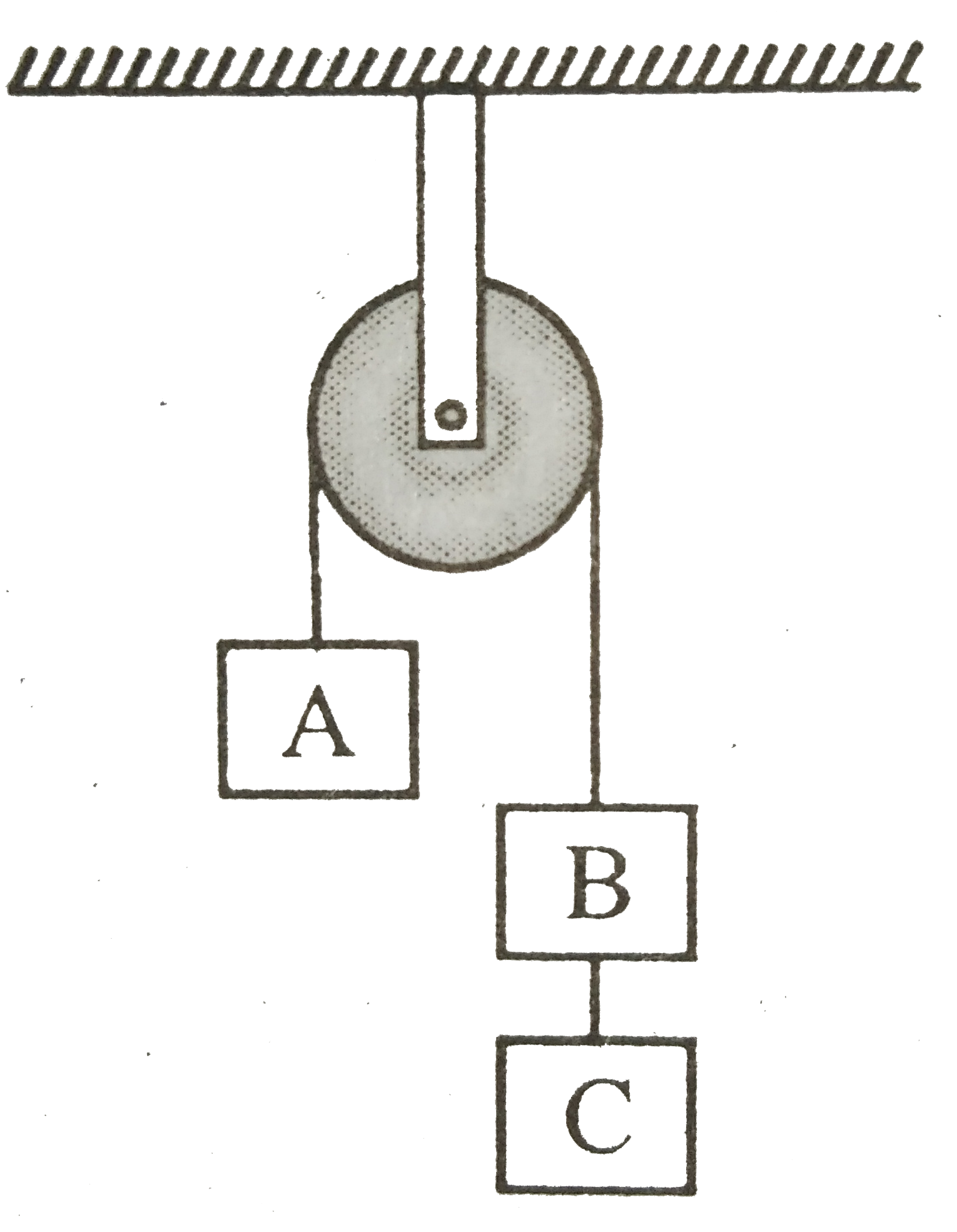
Three objects of identical mass attached to strings are suspended in a large tank of liquid as shown.a Must all three strings have the same tension? ____ Yes ____ No Justify your answer. Object A has a volume of 1.0 x 10-5 m3 and a density of 1300kg m3 The tension in the string to which object A is attached is 0.0098 N.b Calculate the buoyant force on object A. c Calculate the density of the liquid. d Some of the liquid is now drained from the tank until only half of the volume of object A is submerged. Would the tension in the string to which object A is attached increase decrease or remain the same? ____ Increase ____ Decrease ____ Remain the same
a There are three forces acting on the masses in each case. Tension up buoyant force up weight down. Since they are at rest we have. Fnet = 0 Ft + Fb = mg Ft = mg – Fb so the largest Fb makes the largest FtWe are to assume the diagram is to scale and that clearly the volumes of the three containers are different. The one with the largest volume displaces the largest amount and weight of water and will have the largest buoyant force acting on it. So since they all displace different volumes and weights of water they all have different buoyant forces and based on the equation shown above will have different tensions.b The mass of the object is given by m = ρobjVobj. Using the equation from part a Ft + Fb = mg Ft + Fb = ρobjVobj.g 0.0098 + Fb = 13001 x 10–59.8 Fb = 0.1176N c The buoyant force is by definition equal to the weight of the displaced fluid. Fb = ρfluidVdisp. g 0.1176 = ρfluid 1 x 10–59.8 ρfluid = 1200kg/m3 d With only half of the volume submerged ½ as much water will be displaced and the buoyant force will be half the size. Based on the formula from part A less buoyant from will make a larger tension. This also makes sense conceptually. Objects have large apparent weights in air than water so having some of it in the air will increase its apparent weight.
Related Solutions
An object of mass 0.75 kg is hanging from a string attached to roof.What will be the force applies by string on the object?
View SolutionAn object of volume V is immersed in a liquid of density d. Calculate the magnitude of buoyant force acting on the object due to liquid .
View Solutionসমপ্রস্থচ্ছেদের একটি বস্তু একটি তরলে ভাসে। তরলের ঘনত্ব বস্তুর ঘনত্বের তিনগুণ | তরলের ওপরে বস্তুটির সমগ্র আয়তনের যত অংশ থাকে তা হল
View SolutionAn object of mass 10 kg is attached to the ceiling by a string which rotates in a horizontal circle of radius 4m at an inclination of 30° from the vertical. The tension in the string is (approximately)
View SolutionAn object of mass 10kg is attached to roof by string whirled round a horizontal circle of radius 4 and 30^@ to the vertical. The tension in the string (approximately) is
View SolutionAn object of mass 10kg is attached to roof by string whirled round a horizontal circle of radius 4 and and and 30^@ to the vertical. The tension in the string (approximately) is
View Solution2 किग्रा भार के तीन पिंड A, B व C एक स्थिर घिरनी से होकर जाने वाली डोरी से बँधे हैं । पिंड B और C को जोड़ने वाली डोरी में तनाव होगा -
View SolutionAn object of specfic gravity rho is hung from a massless string. The tension in the string is T. The object is immersed in water so that one half of its volume is submerged, the new tension in the string is
View SolutionAn object of specfic gravity Pis hung from a massless string. The tension in the string is T. The object is immersed ir water so that one half of its volume is submerged, the new tension in the string is
View SolutionAn object of mass is tied to a light string wound around a pulley that has a moment of inertia and radius . The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionAn object of mass 0.8 kg is rotated in horizontal circle of radius 0.5m. With help of string 60 r.p.m Find,Tension in string
View SolutionA V-volume object is immersed in a liquid of p density. Calculate the force exerted on the fluid object.
View SolutionA solid object is immersed in water in a vessel by a string attached to the base,immediately on cutting the string,the object travels 1m in 1 sec.The relative density of solid is "(g=10m/s^(2))
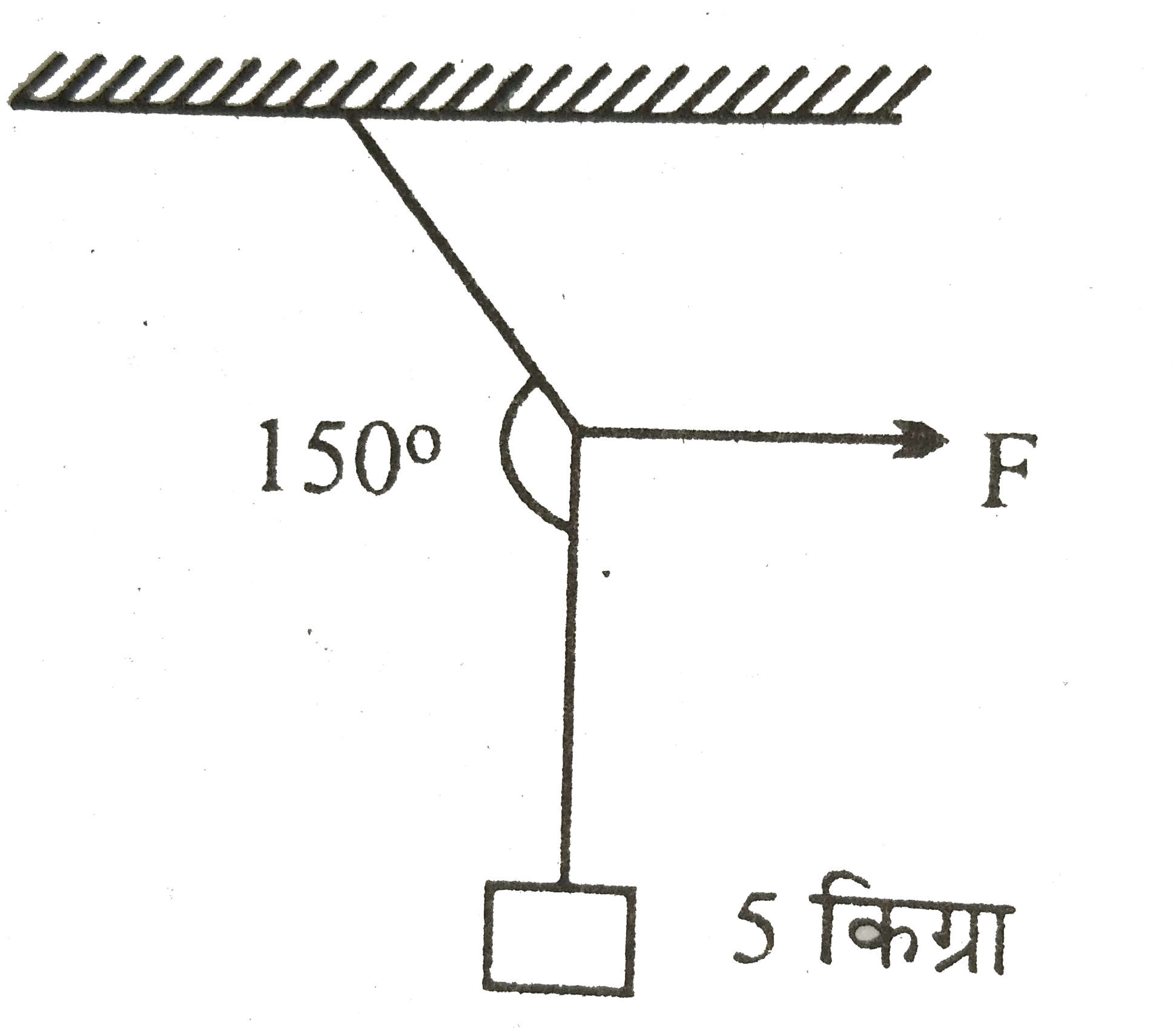
View Solutionचित्र में दर्शाये अनुसार 5 किग्रा द्रव्यमान की एक वस्तु भारहीन डोरी से लटकाई गयी है । उस पर एक क्षैतिज बल f लगाया जाता है जिसके कारण डोरी के दोनों भागों के बीच का कोण बनता है । बल F और डोरी के ऊपरी भाग पर तनाव ज्ञात कीजिए ।
View SolutionAn object of mass 10 kg is whirled round a horizontal circle of radius 4 m by a revolving string inclined to the vertical .if the uniform speed of the object is , the tension in the string (approximate ) is
View SolutionA string of total mass 100g & total length 2m is under tension due to the weight of an object of mass 8kg .If the resulting sinusoidal wave in the string has an amplitude of 6cm and frequency 60Hz the power that must be supplied to the string is
View SolutionA wooden block or mass m and density is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density with . The tension in the string will be
View SolutionA wooden block of mass m and density rho is tied to a string. The other end of the string is fixed to the bottom of a tank. The tank is filled with a liquid of density sigma with sigma lt rho .What is the tension in the string?
View SolutionTransverse waves pass through the strings A and B attached to an object of mass m as shown. If mu is the linear density of each of the strings the velocity of the transverse waves produced in the strings A and B is
View SolutionTransverse waves pass through the strings A and B attached to an object of mass 'm' as shown. If mu is the linear density of each of the strings, the velocity of the transverse waves produced in the strings A and B is
View Solution