A circular disc of mass m and radius T is rotating on a rough surface having coefficient of friction µ with an initial angular velocity ω. Assuming a uniform normal reaction on the entire contact surface the time after which the disc comes to rest isA ωR/µgB 3ωR/4µgC ωR/2µgD √3 ωR/µg
Correct option B 3ωR/4µgExplanation:Consider a small element of disc of thickness dx at a radius x.
Related Solutions
A circular disc of mass m and radius R is rotating on a roach surface , the time after which the disc comes to rest is
View SolutionA disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity initially.
The disc is placed such that axis of both are concident. The coefficient of friction is for surfaces of contact Assume that pressure on disc is uniformely distributed.
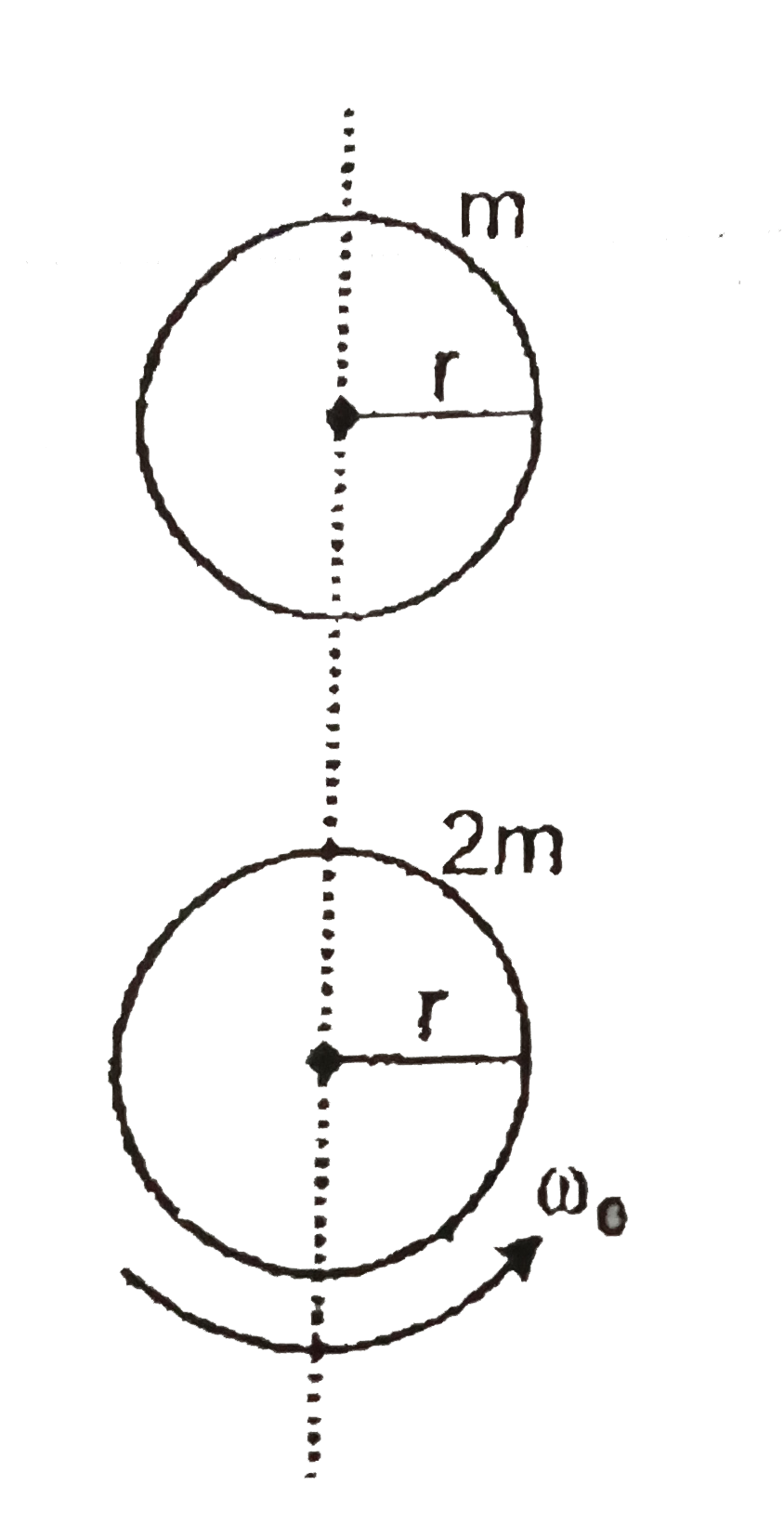
Time elapsed in this process
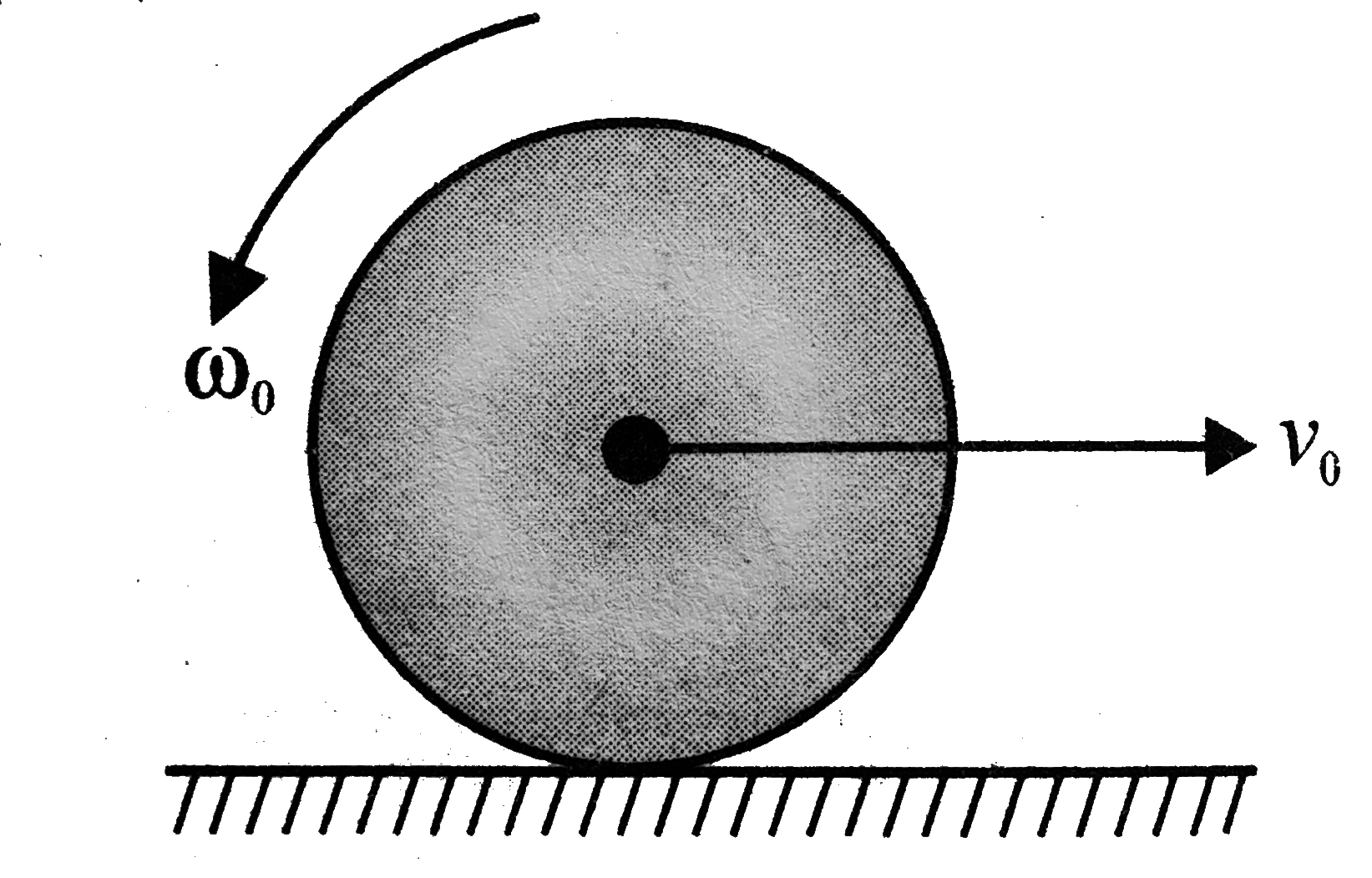
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v_(0) and angular velocity omega_(0) as shown. The disc comes to rest after moving some distance to the right. It follows that
View SolutionA uniform circular disc of radius is placed on a rough horizontal surface and given a linear velocity and angular velocity as shown. The disc comes to rest after moving some distance to the right. It follows that
View SolutionA disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity omega_(0) initially. The disc is placed such that axis of both are concident. The coefficient of friction is mu for surfaces of contact Assume that pressure on disc is uniformely distributed. Angular velocity 'omega' when both discs start rotating together without slipping
View SolutionA uniform circular disc of radius r placed on a rough horizontal plane has initial velocity v_0 and an angular velocity w_0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
View SolutionThe initial velocity of a uniform circular disc of radius r placed on a rough horizontal plane v_0 and angular velocity omega_0 is, as shown. After traveling some distance in the direction of motion, the disc comes to rest. Then:
View SolutionA uniform circular disc of radius . 1placed on a rough horizontal plane has initial velocity and an angular velocity as shown. The disc comes to rest after moving some distance in the direction of motion. Then
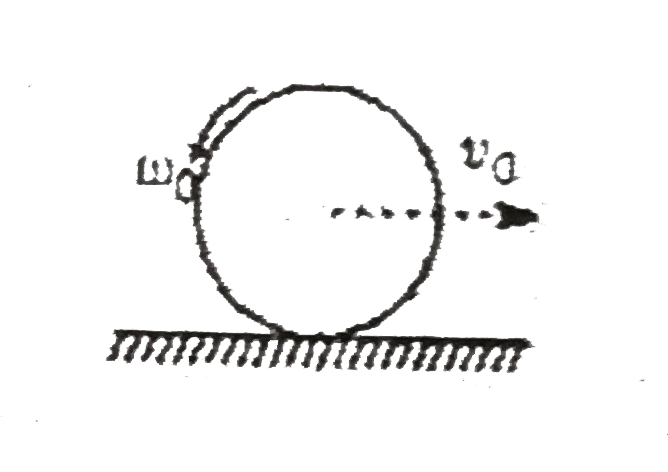
View SolutionA uniform disc of radius is spinned to the angular velocity and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to ? The pressure exerted by the disc on the surface can be regarded as uniform.
View SolutionA uniform disc of radius R is spinned to the angular velocity and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be neglected as uniform.
View SolutionA uniform circular disc of radius r placed on a rough horizontal plane has initial velocity v_(0) and angular omega_(0) as shown. The disc comes to rest after moving some distance in the direction of motion. Then
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
View SolutionA large disc has mass 2kg and radius 0.2 m and initial angular velocity 50 rad/s and small disc has mass 4kg and radius 0.1 m and initial angular velocity 200 rad/s both rotating about their common axis. Then the common final angular velocity after discs are in contact is,
View SolutionA large disc has mass 2kg and radius 0.2 m and initial angular velocity 50 rad/s and small disc has mass 4kg and radius 0.1 m and initial angular velocity 200 rad/s both rotating about their common axis. Then the common final angular velocity after discs are in contact is,
View SolutionA uniform circular disc of mass m and radius R is rolling without slipping on a smooth horizontal surface as shown in figure. The disc collides with a rough vertical wall having coefficient of restitution . If the disc rolls without slipping after collision with the wall, and the coefficient of friction is n/10, then find n.

View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB is and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is .

View SolutionA large disc has mass 2 kg and radius 0.2 m and initial angular velocity 50rad/s and a small disc has mass 4kg and radius 0.1m and initial angular velocity 200 rad/s, both rotating about their common axis. Then the common final angular velocity after discs are in contact is,
View SolutionA rough disc of mass rotates freely with an angular velocity . If another rough disc of mass and same radius but spinning in opposite sense with angular speed is kept on the first disc. Then:
View SolutionA disc of mass m and radius R rotating with angular speed omega_(0) is placed on a rough surface (co-officient of friction =mu ). Then
View Solution