Find the force required to stretch a wire of area of cross section 2x10-4 m2 so that its length becomes 1.5 times original length . Young’s modulus=3.6x1011Nm-2 .
A=2x10-4m 2 Y=3.6x1011Nm-2 Let L original length then ∆L=1.5L- L=0.5L
Related Solutions
What force would be required to stretch a streel wire fo 4 mm^2 cross section, so that its length becomes 3 times its original length ? Given that Young's modulus of the meterial of the steel wire is 2.4 xx 10^(12) dyne // cm^2.
View SolutionWhat force is required to stretch a steel wire to double its length when its area of cross section 1 cm2 and Young.s modulus .
View SolutionThe force required to stretch a steel wire 1cm^(2) in cross - section to increase its length by 1% ,if its Young's modulus is 2xx10^(11)Nm^(-2) ,is
View SolutionA steel wire of length 4.7 m and cross-sectional area stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionA steel wire of length 4.7 m and cross-sectional area stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionIf Y is the Young's modulus of a wire of cross sectional area A, then the force required to increase its length by will be
View SolutionA elongation of 0.1% in a wire of cross-sectional area 10"6 m2 causes tension 100 N. The young’s modulus is
View SolutionConsider a wire of length l, area of cross section A, and resistivity with resistance . Its length is increased by applying a force, and it becomes four times of its original value. Find the changed resistance of the wire.
View SolutionConsider a wire of length l, area of cross section A, and resistivity rho with resistance 10 Omega . Its length is increased by applying a force, and it becomes four times of its original value. Find the changed resistance of the wire.
View SolutionThe area of cross-section of steel wire is 0.1 cm^(2) and Young's modulus of steel is 2 times 10^(11)N" "m^(-1) . The force required to stretched by 0.1% of its length is
View SolutionA wire of resistance 4 Omega is stretched to twice its original length. In the process of stretching, its area of cross-section gets halved. Now, the resistance of the wire is
View SolutionA wire of resistance is stretched to twice its original length. In the process of stretching, its area of cross-section gets halved. Now, the resistance of the wire is
View SolutionA brass wire of length 4.5m with cross-section area of and a copper wire of length 5.0 m with cross section area are stretched by the same load. The same elongation is produced in both the wires. Find the ratio of Young’s modulus of brass and copper.
View SolutionYoung's modulus of steel is Y and its rigidity modulus is eta . A piece of steel of cross-sectional area A, is stretched into a wire of length L and area of cross-section (A)/(4) , In wire case
View SolutionA wire of circular cross-section and 25 Ω resistance is uniformly stretched until its new length is three times the original length. Find its resistance.
View SolutionCross sectional area of a steel wire is 1 cm^2 .How much force is required to increase its length to twice its initial length? Young's modulus for steel is 2 times 10^12 dyn.cm^-2 .
View SolutionY is the Young's modulus of the material of a wire of length L and cross-sectional area A. It is stretched through a length l. What is the force constant of the wire?
View SolutionIf a wire of length 4 m and cross-sectional area of is stretched by a force of 3 kN, then determine the change in length due to this force . Given, Young's modulus of material of wire is
View SolutionIf a wire of length 4 m and cross-sectional area of is stretched by a force of 3 kN, then determine the change in length due to this force . Given, Young's modulus of material of wire is
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Match the following two columns.
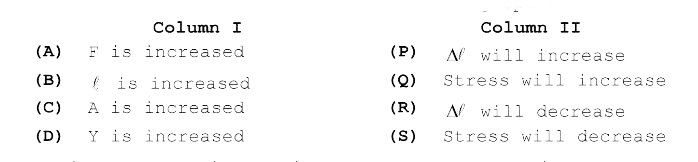
View Solution