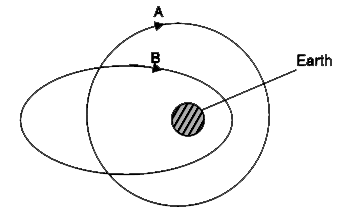
A satellite of mass m is in an elliptical orbit around the Earth which has mass Me and radius Re. The orbit varies from a closest approach of distance a at point A to maximum distance of b from the center of the Earth at point B. At point A the speed of the satellite is vo. Assume that the gravitational potential energy Ug = 0 when masses are an infinite distance apart. Express your answers in terms of a b m Me Re vo and G. a. Determine the total energy of the satellite when it is at A. b. What is the magnitude of the angular momentum of the satellite about the center of the Earth when it is at A? c. Determine the velocity of the satellite as it passes point B in its orbit.As the satellite passes point A a rocket engine on the satellite is fired so that its orbit is changed to a circular orbit of radius a about the center of the Earth. d. Determine the speed of the satellite for this circular orbit. e. Determine the work done by the rocket engine to effect this change.
a. E = PE + KE = - GMeM/a + 1/2mv02b. L = mvr = mv0ac. Conservation of angular momentum gives mv0a = mvbb or vb = v0a/bd. Fg = Fe gives GMm/R2 = mv2/R = and v = √GMe/ae. The work done is the change in energy of the satellite. Since the potential energy of the satellite is constant the change in energy is the change in kinetic energy or W = ∆KE = 1/2mGMe/a - v02
Related Solutions
A satellite of mass m is in an elliptical orbit around the earth of mass M(M gt gt m) the speed of the satellite at its nearest point ot the earth (perigee) is sqrt((6GM)/(5R)) where R= its closest distance to the earth it is desired to transfer this satellite into a circular orbit around the earth of radius equal its largest distance from the earth. Find the increase in its speed to be imparted at the apogee (farthest point on the elliptical orbit).
View SolutionA satellite of mass m is in an elliptical orbit around the earth of mass M(M gt gt m) the speed of the satellite at its nearest point ot the earth (perigee) is sqrt((6GM)/(5R)) where R= its closest distance to the earth it is desired to transfer this satellite into a circular orbit around the earth of radius equal its largest distance from the earth. Find the increase in its speed to be imparted at the apogee (farthest point on the elliptical orbit).
View SolutionA satellite of mass m is in an elliptical orbit around the earth of mass M(M gt gt m) the speed of the satellite at its nearest point ot the earth (perigee) is sqrt((6GM)/(5R)) where R= its closest distance to the earth it is desired to transfer this satellite into a circular orbit around the earth of radius equal its largest distance from the earth. Find the increase in its speed to be imparted at the apogee (farthest point on the elliptical orbit).
View Solutionm द्रव्यमान का एक उपग्रह पृथ्वी ( द्रव्यमान M ) के चारों ओर r त्रिज्या की कक्ष में घूम रहा है । कक्ष के केंद्र के परितः उपग्रह का कोणीय संवेग होगा -
View SolutionSatellite A is following a circular path of radius a around the earth another satellite B follows an elliptical path around the earth. The two satellites have same mechanical energy and their orbits intersect. Find the speed of satellite B at the point where its path intersects with the circular orbit of A. Take mass of earth to be M.
View SolutionThe minimum and maximum distances of a satellite from the center of the earth are and respectively, where is the radius of earth and is the mass of the earth . Find
(a) its minimum and maximum speeds,
(b) radius of curvature at the point of minimum distance.
View SolutionThe minimum and maximum distances of a satellite from the center of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth . Find (a) its minimum and maximum speeds, (b) radius of curvature at the point of minimum distance.
View SolutionIf a satellite is revolving around a planet of mass M in an elliptical orbit of semi-major axis M, then find the orbital speed of the satellite when it is at a distance from the focus.
View SolutionA satellite of mass 'm' is revolving in a circular orbit of radius 'r' around the earth of mass M. What is the total energy of the satellite?
View Solutionएक उपग्रह S दीर्घवृतीय कक्षा में पृथ्वी का परिक्रमा कर रहा है। उपग्रह का द्रव्यमान पृथ्वी के द्रव्यमान की तुलना में बहुत कम है, तो
View Solutionएक उपग्रह S, दीर्घवृत्तीय कक्षा में पृथ्वी की परिक्रमा कर रहा है | उपग्रह का द्रव्यमान, पृथ्वी के द्रव्यमान की तुलना में बहुत कम है तब
View SolutionA satellite S is moving in an elliptical orbit around the earth the mass of the satellite is very small compared to the mass of the earth then
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA satellits S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth
View SolutionA satellite S moving in an elliptical orbit around the earth the mass of satellite is very small compared to the mass of the earth then
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth
View SolutionA satellite S is revolving around the earth in an elliptical orbit, then the mass of the satellite is very less than the mass of the earth.
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA satellite S moving in an elliptical orbit around the earth the mass of satellite is very small compared to the mass of the earth then
View Solution