A particle has a velocity u towards east at t = 0. Its acceleration is towards west and is constant. Let xA and xB be the magnitude of displacements in the first 10 seconds and the next 10 secondsa xA XBd the information is insufficient to decide the relation of xA with xB.
d the information is insufficient to decide the relation of xA with xB.Explanation:Magnitude of displacement depends up on initial velocity time Duration and acceleration. In this case only time is known while magnitude of initial velocity and acceleration is unknown. These two displacements could only be comparable if directions of initial velocity and acceleration had been the same. Since in this case directions are opposite their magnitudes need to be known So there is not sufficient information.
Related Solutions
A particle has a velocity u towards east at . Its acceleration is towards west and is constant. Let and be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionA particle has a velocity u towards east at . Its acceleration is towards west and is constant. Let and be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionA particle has a velocity u towards east at . Its acceleration is towards west and is constant. Let and be the magnitude of displacement in the first 10 seconds and the next 10 seconds:
View SolutionA particle has a velocity u towards east at . Its acceleration is towards west and is constant. Let and be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionXA+XB होगा
View SolutionXA+XB will be
View SolutionIf f(x) = |{:(0,xa,xb),(xa,0,xc),(xb,xc,0):}| , Then
View Solutionint (dx) / ((xa) (xb))
View Solutionযদি a, b, c বাস্তব হয়, তবে (x-b)(x-c) + (x-c)(x-a) + (x-a)(x-b) =0 সমীকরণের উভয় বীজ সর্বদা
View Solutionint (dx) / ((xa) ^ (2) (xb))
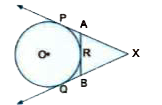
View SolutionIn the Fig Prove that XA+AR=XB+BR.
View Solutionint (dx) / ((xb) ^ (3) (xa) ^ (2))
View Solutionint (dx) / (sin (xa) sin (xb))
View Solutionint (1) / (sin (xa) cos (xb)) dx =
View Solutionint (dx) / (sin (xa) sin (xb))
View Solutionint ((1) / ((sin xa) sin (xb))) dx
View Solutionके गुणनखंड है :
View Solutionसमय t = 0 पर एक कण का वेग पूर्व की ओर v है | इसका त्वरण एकसमान है और पश्चिम की ओर है |कण का विस्थापन पहले 10 सेकंड में तथा अगले 10 सेकंड में है , तो
View Solutionयौगिक XA, XB, XC को A, B,C विलयन रखने वाली परखनलियों में डाला जाता है। XB, A और C के साथ क्रिया करता है। XA इनमें से किसी के साथ क्रिया नहीं करता है। XC,A के साथ क्रिया करता है।
ऋणायनों को उनके ऑक्सीकरण के घटते हुए क्रम में व्यवस्थित कीजिए।
View Solutionनिम्नलिखित फलनों का x के सापेक्ष अवकल गुणांक निकालें।
(x-a)(x-b), जहाँ a और b अचर हैं
View Solution