A 300-kg box rests on a platform attached to a forklift shown. Starting from rest at time = 0 the box is lowered with a downward acceleration of 1.5 m/s2 a. Determine the upward force exerted by the horizontal platform on the box as it is lowered. At time t = 0 the forklift also begins to move forward with an acceleration of 2m/s2 b. Determine the frictional force on the box. while lowering the box as described above. The box does not slip or tip over. c. Given that the box does not slip determine the minimum possible coefficient of friction between the box and the platform. d. Determine an equation for the path of the box that expresses y as a function of x and not of t assuming that at time t = 0 the box has a horizontal position x = 0 and a vertical position y = 2m above the ground with zero velocity.e. On the axes below sketch the path taken by the box
a. ΣF = ma; using downward as the positive direction mg – N = may gives N = mg – ay = 2490Nb. Friction is the only horizontal force exerted; ΣF = f = max = 600Nc. At the minimum coefficient of friction static friction will be at its maximum value f = µN giving µ = f/N = 600N/2490N = 0.24
Related Solutions
A 45 kg box starts from rest and moves on a smooth plane the force that varies with time as shown. The velocity of the box at t=8 sec is:
View SolutionA box of bananas weighing rests on a horizontal surface is and the coefficient of kinetic friction is
a. If no horizontal force is applied to the box and the box is at rest , how large is the friction force excered on the box ?
b. What is the magnitude of the friction forces if a monkey applies a horizontal force of to the box and the box is initial at rest?
c. What minimum horizontal force must the monkey apply to start the box in motion ?
d. What minimum horizontal force must the monkey apply to keep the box moving at constant velocity once it has been starts?
e. If the monkey applies a horizontal force of What is the magnitude of the friction force and what is the box's acceleration ?
View SolutionA box of bananas weighing rests on a horizontal surface is and the coefficient of kinetic friction is
a. If no horizontal force is applied to the box and the box is at rest , how large is the friction force excered on the box ?
b. What is the magnitude of the friction forces if a monkey applies a horizontal force of to the box and the box is initial at rest?
c. What minimum horizontal force must the monkey apply to start the box in motion ?
d. What minimum horizontal force must the monkey apply to keep the box moving at constant velocity once it has been starts?
e. If the monkey applies a horizontal force of What is the magnitude of the friction force and what is the box's acceleration ?
View SolutionWhat should be the acceleration a of the box shown in figure so that the block of mass m exerts a force (mg)/(4) on the force of the box?
View SolutionWhat should be the acceleration a of the box shown in figure so that the block of mass m exerts a force (mg)/(4) on the force of the box?
View SolutionA box of mass m is placed on a smooth horizontal platform as shown in the figure. The platiform is made to move in direction above the horizontal with acceleration a so that the contact force between the box and the platform becomes 3 mg/2. Find the magnitude of the acceleration.

View SolutionA box of mass m is placed on a smooth horizontal platform as shown in the figure. The platiform is made to move in direction above the horizontal with acceleration a so that the contact force between the box and the platform becomes 3 mg/2. Find the magnitude of the acceleration.

View SolutionA box of mass m is placed on a smooth horizontal platform as shown in the figure. The platiform is made to move in direction above the horizontal with acceleration a so that the contact force between the box and the platform becomes 3 mg/2. Find the magnitude of the acceleration.

View SolutionA box wegihing 100N is at rest on a horizontal floor. The coefficient of static friction between the box and the floor is 0.4. What is the smallest force F exected and upward at an angle 30^@ with the horizontal that can start the box in motion?
View SolutionFigure shows a boy on a horizontal platform A on a smooth horizontal surface, holding a rope attached to a box B. Boy pulls the rope with a constant force of 50 N. The combined mass of platform A and boy is 250kg and that' of box B is 500kg. The velocity of A relative to the box B 5 s after the boy on A begins to pull ,the rope,will be:
View SolutionFind force required in accelerating a 3 kg mass at 5 m/s2 and a 4 kg mass at 4 m/s2
View Solutionकिसी क्षैतिज टेबल पर विराम में रखे 10 kg द्रव्यमान के बॉक्स पर विचार कीजिए तथा गुरूत्व के कारण त्वरण लीजिए
(a) बॉक्स का बल निर्देशक आरेख (FBD) बनाइये ।
(b) बॉक्स पर टेबल द्वारा आरोपित बल का मान ज्ञात कीजिए।
(c) टेबल पर बॉक्स द्वारा आरोपित बल का मान ज्ञात कीजिए।
(d) क्या बॉक्स पर टेबल द्वारा आरोपित बल तथा बॉक्स का भार तृतीय नियम का क्रिया- प्रतिक्रिया युग्म बनाते हैं?
View SolutionA worker uses a forklift to move boxes that weigh either 40 pounds or 65 pounds each. Let x be the number of 40-pound boxes and y be the number of 65-pound boxes. The forklift can carry up to either 45 boxes or a weight of 2,400 pounds. Which of the following systems of inequalities represents this relationship?
View Solutionएक स्प्रिंग पर विचार कीजिए जिसका एक सिरा स्थिर आधार से तथा दूसरा सिरा एक बॉक्स से जुड़ा है। बॉक्स चित्रानुसार चिकने फर्श पर विराम में रखा है । बॉक्स के द्रव्यमान को m से , स्प्रिंग के बल नियतांक को k से तथा गुरूत्वीय त्वरण को g से व्यक्त करें । बॉक्स को क्षैतिज रूप से धकेलकर स्थिर आधार की ओर x दूरी तक विस्थापित करके विराम में रख देते हैं ।
(a) बॉक्स का बल निर्देशक आरेख बनाइये ।
(b) बॉक्स पर हाथ द्वारा आरोपित बल ज्ञात कीजिए ।
(c) न्यूटन के तृतीय नियम के सभी क्रिया-प्रतिक्रिया युग्मों को लिखिए ।
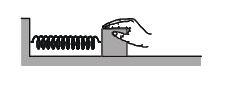
View SolutionConsider a spring whose one end is attached to a fixed base and the other end to a box. The box is kept at rest on a smooth floor as shown in the figure. Express the mass of the box by m, the force constant of the spring by k and the acceleration due to gravity by g. The box is pushed horizontally towards the fixed base by displacing it by a distance x and put it at rest. (a) Draw a free body diagram of the box. (b) Find the force exerted by the hand on the box. (c) Write down all the action-reaction pairs of Newton's third law.
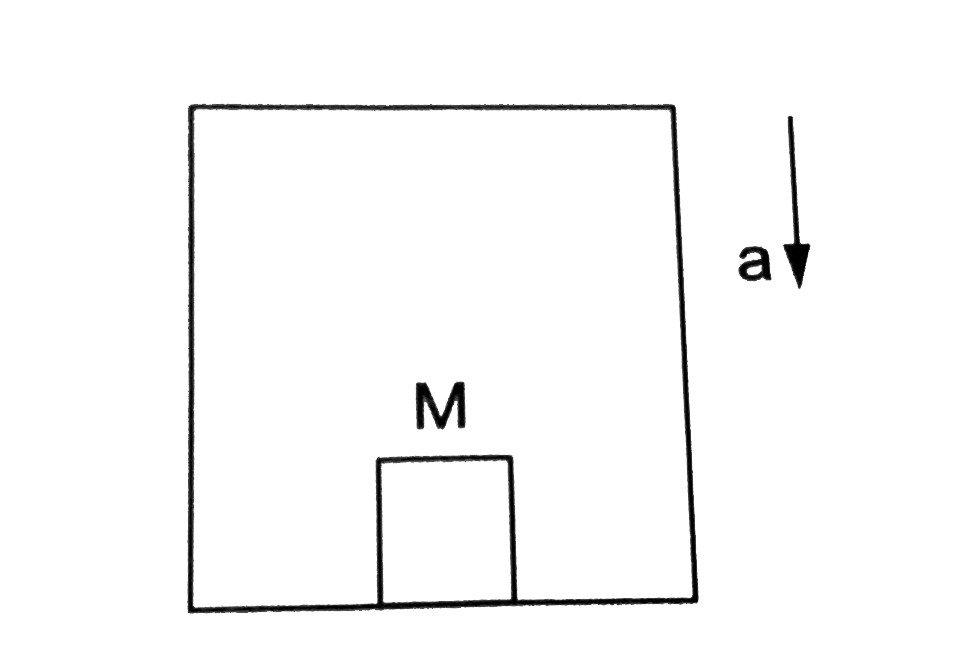
View Solutionचित्र में एक बड़े बॉक्स को नीचे की ओर a त्वरण से गिरता हुआ दिखाया गया है। बॉक्स के अंदर M द्रव्यमान की एक वस्तु रखी है। त्वरण a का मान कितना होना चाहिए ताकि बॉक्स के फर्श पर बल लगाए?
View Solutionएक 800 kg द्रव्यमान का रेल इंजन प्रति 2000 kg द्रव्यमान लाले पाँच डिब्बो को सीधी पत्री पर खींचता है | यदि इंजन 40000 N का बल आरोपित करता है तथा यदि पटरी 5000 N का घर्षण बल लगाती है तो ज्ञात करें -
(a) नेट त्वरण बल (b) रेल का त्वरण तथा
(c) डिब्बा 1 द्वारा डिब्बा 2 पर लगाया गया बल |
View SolutionIn the previous problem if M=80kg and m=410kg and the boy pulls the rope such that the system (boy+box) moves upward with acceleration 5m//s^(2) ,find the force exerted by the boy and contact force between the boy and the box.
View SolutionA 2kg box sits on a 3kg box which sits on a 5kg box.The 5kg box rests on a table.What is normal force exerted by 5kg box on the 3kg box?
View SolutionTwo boxes A and B of masses m and M interconnected by an ideal rope and ideal pulleys are held at rest as shown. When it is released, box B accelerates downwards. Find velocities of box A and B as function of time t after system has been released.
View Solution