In triangle ABC let AD BE and CF be the internal angle bisectors with D E and F on the sides BC CA and AB respectively. Suppose AD BE and CF concur at I and B D I F are concyclic then ∠IFD has measure – A 15° B 30° C 45° D Any value < 90°
Correct option B 30° Explanation:
Related Solutions
In triangle ABC, let AD, BE and CF be the internal angle bisectors with D, E and F on the sides BC, CA and AB respectively. Suppose AD, BE and CF concur at I and B, D, I, F are concyclic, then has measure-
View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the , then is
View Solutionकी भुजाओ BC, CA,AB के मध्य D,E ,F बिंदु है , तो
View SolutionABC एक समबाहु त्रिभुज है AB , BC CA भुजाओं पर क्रम्स: D , E और F मध्य बिंदु लिए गए है ताकि AD =BE -CF होगा तुह AE BF , CD द्वारा निर्मित त्रिभुज होगा कैसा होगा
View SolutionConsider Let I be the incentre and a,b c be the sides of the triangle opposite to the angle A,B,C respectively. Let O be any point in the plane of within the triangle . AO ,BO ,CO meet the sides BC, CA and AB in D, E and F respectively then
View SolutionIf are the mid points of the side and respectively of a triangle ABC, write the value of
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
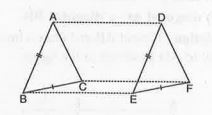 Show that and AD=CF.
Show that and AD=CF.
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that and AD=CF.
Show that and AD=CF.
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a and O is any point, show that
(i) AD+BE+CF=0
View SolutionIn ABC, AD, BE and CF are altitudes. Prove I, that,
View SolutionIn ABC, AD, BE and CF are altitudes. Prove I, that,
View SolutionLet A, B, and C be the vertices of a triangle. Let D, E, and F be the midpoints of the sides BC, CA, and AB respectively. Show that .
View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionLet ABC be a triangle such that AB = 4, BC = 5 and CA = 6. Choose points D,E,F on AB, BC, CA respectively, such that AD = 2, BE = 3, CF=4. Then is
View SolutionIf D, E, F are the midpoints of sides BC, CA, AB of triangle ABC and G is the centroid then match the following
View SolutionInternal bisector of an angle of triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent the sides of DABC then
View SolutionIn is the bisector of meeting BC at D, and E is the mid-point of AC. Then median of the triangle is
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the , then is
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the , then is
View Solution