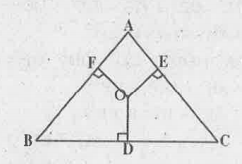
O is any point in the interior of ∆ABC. Bisectors of ∠AOB ∠BOC and ∠AOC intersect side AB side BC side AC in F D and E respectively.Prove that BF × AE × CD = AF × CE × BD
In ∆ AOB OF is bisector of ∠ AOB∴ OA / OB = AF / B ...... 1 by angle bisector theoremIn ∆ BOC OD is bisector of angle ∠ BOC.∴ OB / OC = BD / CD ....... 2by angle bisector theoremIn ∆ AOC OE is bisector of angle∠ AOC.∴ OC / OA = CE / AE ....... 3by angle bisector theorem∴ BF × AE × CD = AF × CE × BD
Related Solutions
If are three points on the sides respectively, of a triangle such that the
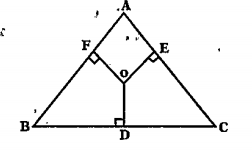
View SolutionIn Fig. the incircle of △ABC, touches the sides BC, CA and AB at D, E respectively. Show that : AF + BD + CE = AE + BF + CD = ½ (Perimeter of △ABC).
View SolutionO is any point in the interior of . Bisectors of and AOC intersect sideAB, side BC, side AC in F,D and E respectively.
Prove that .
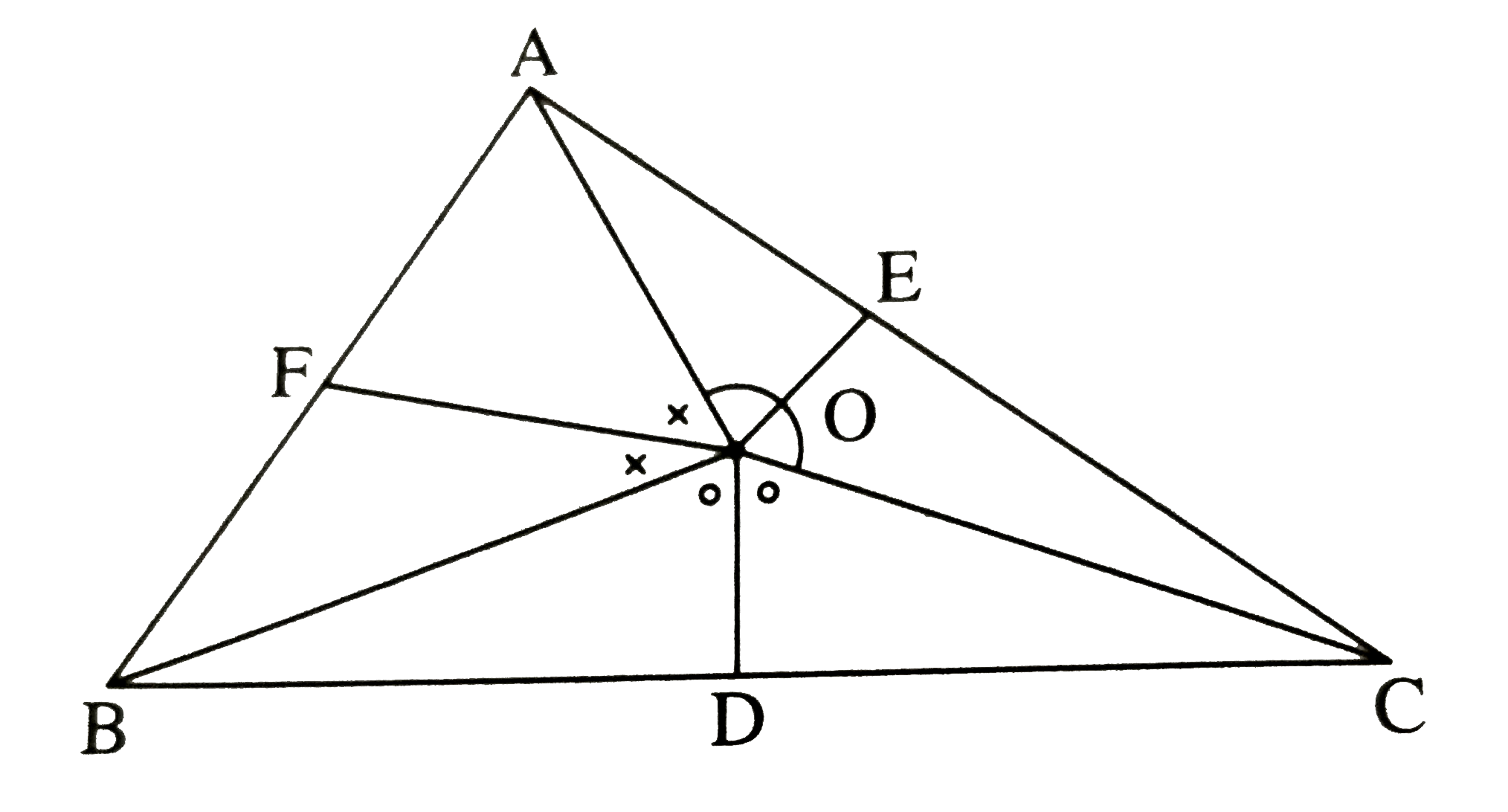
View SolutionIn the given figure, D, E and F are the points where the incircle of the DeltaABC touches F the sides BC, CA and AB respectively. Show that AF+ BD + CE = AE + BF + CD = (perimeter of Delta ABC)
View SolutionO is a point in the interior of ∆ABC . OD,OE and OF are the perpendicular drawn to the sides BC, CA and AB respectively. Prove that AF^2+BD^2+CE^2=AE^2+BF^2+CD^2 .
View SolutionIf D, E and F are three points on the sides BC, CA and AB, respectively, of a triangle ABC such that the lines AD, BE and CF are concurrent, then show that
View SolutionIf D, E and F are three points on the sides BC, CA and AB, respectively, of a triangle ABC such that the lines AD, BE and CF are concurrent, then show that
View SolutionIn Fig. 10.19, the incircle of touches the sides and and respectively. Show that (FIGURE)
View SolutionIn Figure 6.22, the line segment DF intersects the side AC of the triangle ABC at point E in such a way that E is the midpoint of the side AC and angle AEF=angle AFE is. Prove that (BD)/(CD)=(BF)/(CE) is.
View SolutionO' is any point in the interior of a triangle ABC. , and , Show that
.
View SolutionABC is an equilateral triangle. D is a point on the side AC. AD = (1)/(3) E is a point on AC and side BC CE = (1)/(3) BC. BD and AE intersect at F then angleCFB How many degrees will the angle be?
View SolutionThe in circle of touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD BC, OE AC and OF AB. Show that:- .
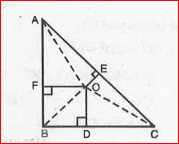 .
.
View SolutionThe straight line parallel to the side of intersects the sides and at the points and respectively. Then .
View Solutionमें अन्तःकोण का समद्विभाजक , भुजा BC को बिंदु D पर काटती है ओर बहिष्कोंण की समद्विभाजक BC को आगे बढ़ाने पर बिंदु E पर मिलता है।
सिद्ध कीजिए कि,
View SolutionDeltaABC The inner circle touches the sides BC, CA and AB on D, E and F respectively. Prove that AF+BD+CE=AE+CD+BF=1/2(DeltaABC The perimeter of )
View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' మరియు అయిన అని చూపండి.
View SolutionIn the ABC, D and E are points on side AB and AC respectively such that DE II BC. If AE=2cm, AD=3cm and BD=4.5cm, then find CE.
View SolutionIn the ∆ABC, D and E are points on side AB and AC respectively such that DE II BC. If AE=2cm, AD=3cm and BD=4.5cm, then find CE.
View SolutionIn the ∆ABC, D and E are points on side AB and AC respectively such that DE II BC. If AE=2cm, AD=3cm and BD=4.5cm, then find CE.
View Solution