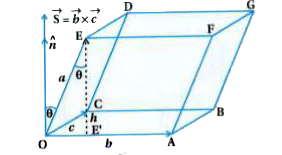
Show that a. b × c is equal in magnitude to the volume of the parallelepiped formed on the three vectors a b and c.
A parallelepiped with origin O and sides a b and c is shown in the following figure.Let cap n be a unit vector perpendicular to both b and c. Hence cap n and a have the same direction.
Related Solutions
Show that is equal in magnitude to the volume of the parallelepiped formed on the three vectors , a, b and c.
View SolutionShow that a.(b × c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors , a, b and c.
View SolutionShow that is equal in magnitude to the volume of the parallelepiped formed on the three vectors a, b and c.
View SolutionShow that is equal in magnitude to the volume of the parallelepiped formed on the three vectors a, b and c.
View Solutionprove that three vectors vec(a), vec(b) And vec(c) Volume of a parallelepiped (vec(a) xx vec(b))* vec(c) is equal to the magnitude of .
View SolutionShow that is equal in magnitude to the volume of the parallelopiped formed on the three vectors a, b and c.
View SolutionVolume of parallelepiped formed by vectors and is 36 then find the volume of parallelepiped formed by the vectors and
View SolutionShow that is equal in magnitude to the volume of the parallelopiped formed on the three vectors,
View SolutionIf are mutually perpendicular vectors of equal magnitudes, show that the vector is equally inclined to and .
View SolutionIf are mutually perpendicular vectors of equal magnitudes, show that the vector is equally inclined to and .
View SolutionShow that a*(bxxc) The magnitude of is equal to the volume of the six heads parallel to the three vectors a, b and c.
View SolutionVolume of parallelepiped determined by vectors vec a,vec b and vec c is 5. Then the volume of the parallelepiped determined by vectors 3(vec a+vec b),(vec b+vec c) and 2(vec c+vec a) is
View SolutionIf the volume of the parallelepiped formed by three non-coplanar vectors is 4 cubic units, then
View SolutionFind the volume of a parallelepiped having three vectors of equal magnitude and equal inclination with each other.
View SolutionIf are three mutually perpendicular vectors of equal magnitude , show that , vectors make an equal angle with
View SolutionShow that is equal in magnitude to the volume of the parallelpiped formed by the vectors
View SolutionShow that veca.(vecbxxvec c) is equal in magnitude to the volume of the parallelpiped formed by the vectors veca,vecb and vec c
View Solutionand are three non zero, non planar vectors. and . The volume of the parallelepiped formed by the vectors and is and the volume of the parallelepiped formed by the vectors and is then = .............
View SolutionIf are three mutually perpendicular vectors of equal magnitude, then the angle which makes with any one of three given vectors, is given by
View SolutionIf a,b and c are three mutually perpendicular vectors of equal magnitude then the angle which a + b + c makes with any one of three given vectors is given by
View Solution