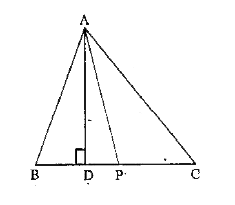
∆ ABC is an equilateral triangle. P is the point on side BC such that PC = 1 / 3 BC. If AB = 6 cm then find AP.
PC = 1 / 3 BC AB = 6∆ ABC is an equilateral triangle.∴ AB = BC = AC = 6∴ PC = 1 / 3 BC = 1 / 3 × 6 = 2 Draw Seg AD ⊥ Seg BC.In ∆ DAC ∠ ADC = 90˚ ∠ACB = 60˚ ∴ ∠DAC = 30˚∴ DC = 1/2 × AC = 1/2 × 6 = 3 .........30o 60o 90o theorem ∴ DP = DC - PC = 3 - 2 = 1.Now AD = √3 / 2 × AC = √3 / 2 × 6 = 3 √3In ∆ ADP AP2 = AB2 + DP2 .............Pythagoras theorem = 3 √3 2 + 12 = 9 × 3 + 1 = 28 ∴ AP = √28 = 2 √7 cm
Related Solutions
is an equilateral triangle. Point P is on base BC such that , if AB = 6 cm, find AP.
is an equilateral
(ii) AB = 6 cm
View Solutionis an equilateral triangle. Point P is on base BC such BC, if AB=6 cm find AP.
View Solutionis an equilateral triangle. Point P is on base BC such that BC, if cm find AP.
View Solutionis an equilateral triangle. Point P is on base BC such that PC=, if AB=6 cm, find AP.
View SolutionDelta ABC is an equilateral triangle.Point P is on base BC such that PC=(1)/(3)BC, if AB=6cm find AP.
View SolutionABC is an equilateral triangle, P is a point in BC such that BP : PC =2 : 1.
Prove that :
View Solutionत्रिभुज ABC की भुजाओं AB तथा AC पर क्रमशः बिंदु P तथा Q इस प्रकार है की है| यदि AP = 2 .4 सेमि., AQ =2 सेमि ., QC =3 सेमि. तथा BC = 6 सेमि., हो तो AB तथा PQ का मान ज्ञात करो|
View SolutionIn , AP is a median on side BC. If AP=7,, find BC.
View Solutionमें, भुजाओं AB तथा AC पर क्रमशः P तथा Q बिन्दु इस प्रकार हैं कि . यदि AP = 4 सेमी. , PB = 6 सेमी. तथा PQ=3 सेमी. हो तो BC ज्ञात कीजिए।
View SolutionThe equilateral triangle ABC is inscribed in a circle. If P is any point on the ar BC, then prove that .
View SolutionThe side BC of an equilateral is parallel to X - axis . Find the slopes of line along sides BC , CA and AB .
View SolutionM is the midpoint of side AB of equilateral triangle ABC.P is a point on BC such that (AP+PM) is minimum.If AB=20 then AP+PM is
View SolutionA circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is:
एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View Solutionis an equilateral triangle . D is a point on the side BC such that . Prove that
View SolutionP is an interior point of an equilateral triangle ABC. If P equidistant from AB and BC, BC and AC, then = _____
View Solutionमें भुजाओं AB तथा AC पर क्रमशः बिंदु P तथा Q है । जबकि PQ BC यदि AP =3 सेमी., PB = 5 सेमी., तथा AC = 8 सेमी. हों, तो AQ की माप ज्ञात करें।
View SolutionIf P, Q, R are the mid-point of the sides AB, BC and CA of respectively, then
View SolutionIn perpendiculars AP and CQ are droped from vertices A and C on opposite sides BC and AB, respectively. If find PQ .
View Solution, समबाहु त्रिभुज है। भुजा BC पर एक बिंदु D इस प्रकार है कि है। यदि है, तो त्रिभुज की भुजा ज्ञात करें।
View SolutionIn , P is mid point of BC, then
AP is a …….of
View Solution