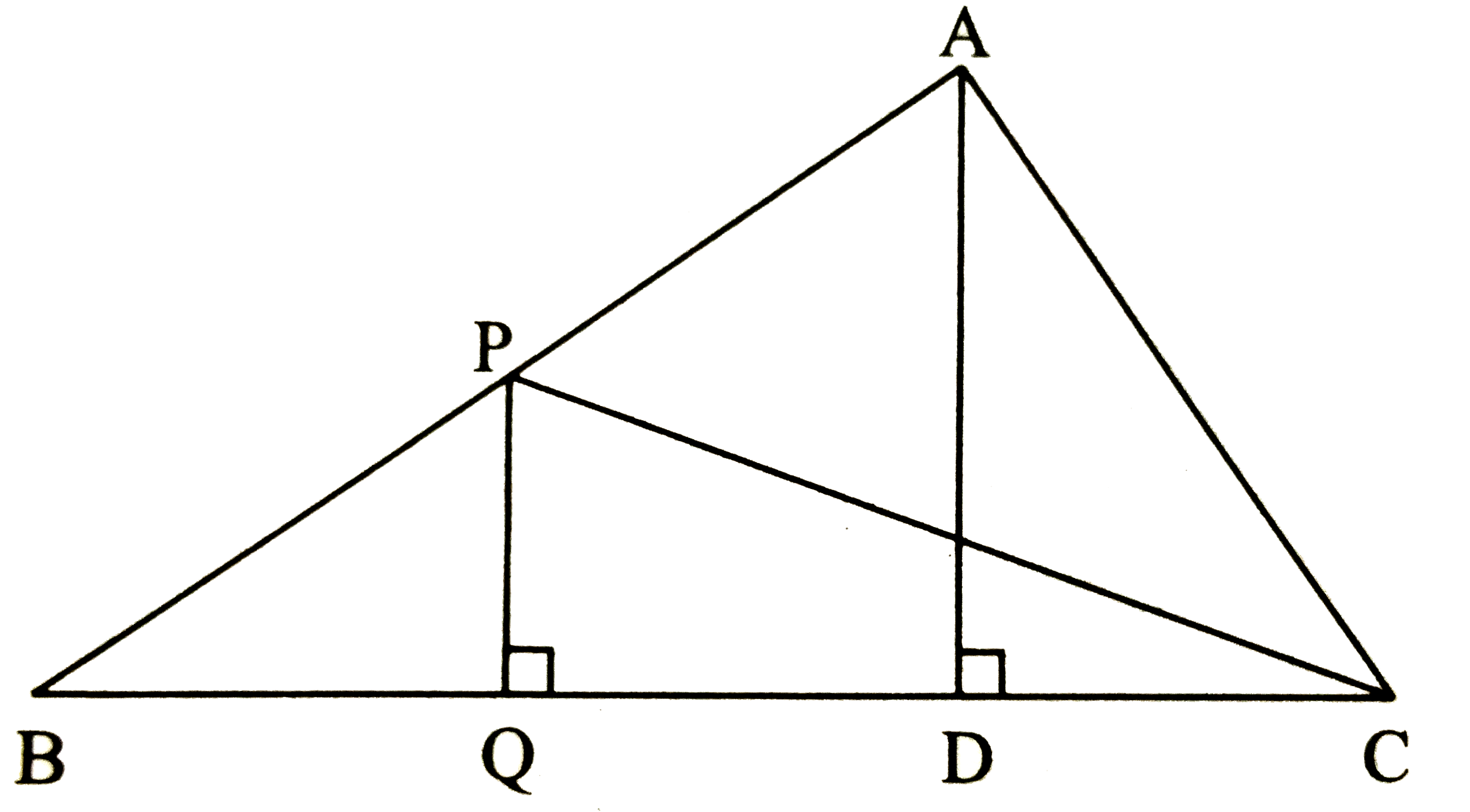
In the adjoining figure PQ ⊥ BC AD ⊥ BC PQ = 4 AD = 6 Write down the following ratios.i A∆PQB / A∆ADBii A∆PBC / A∆ABC
i In ∆PQB and ∆ADB ∠B ≅ ∠B∠PQB ≅ ∠ADB ................. each right angle∴ ∆PQB ∼ ∆ADB ................. A-A test of similarity
Related Solutions
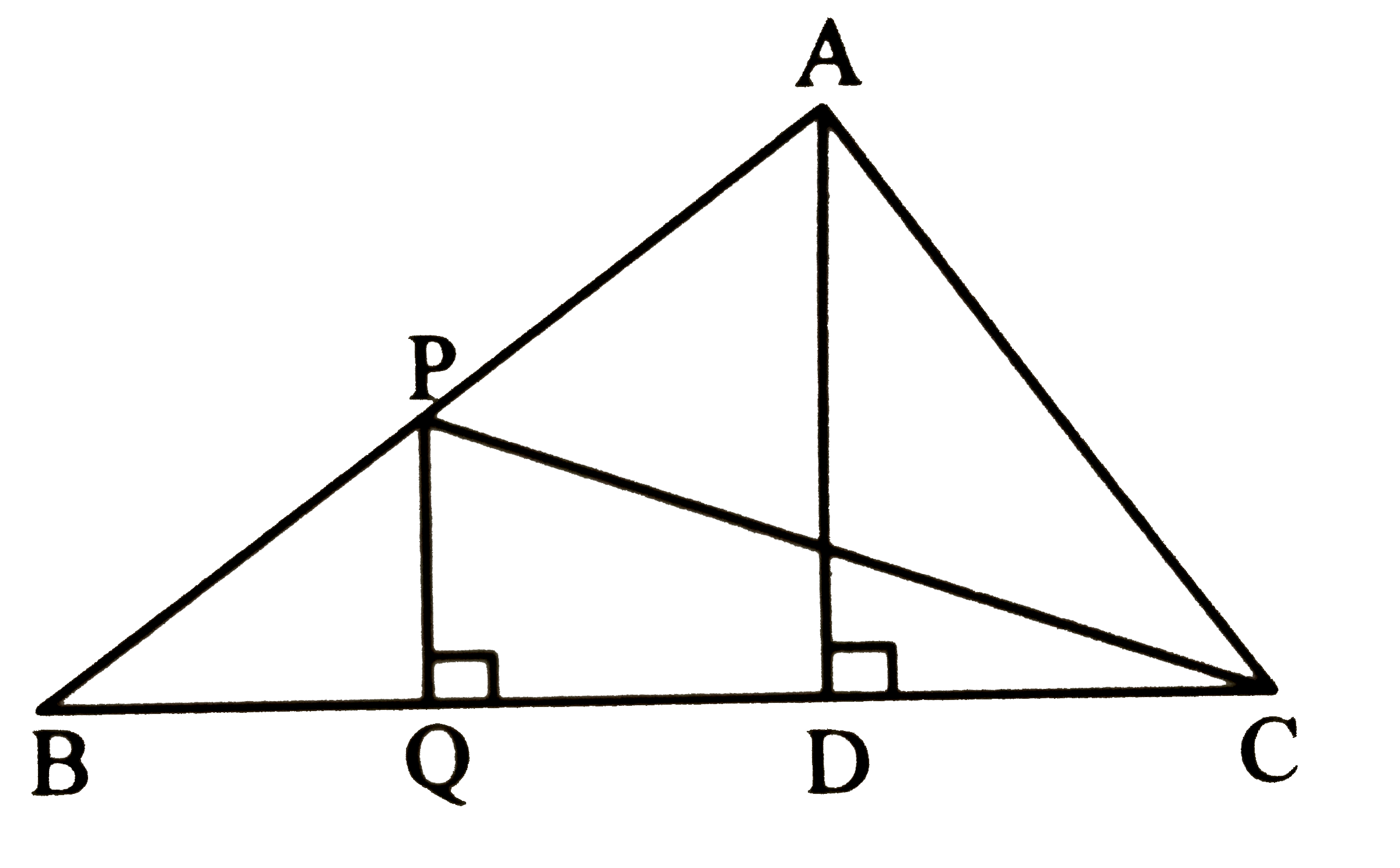
In the adjoining figure, then find ratio
.
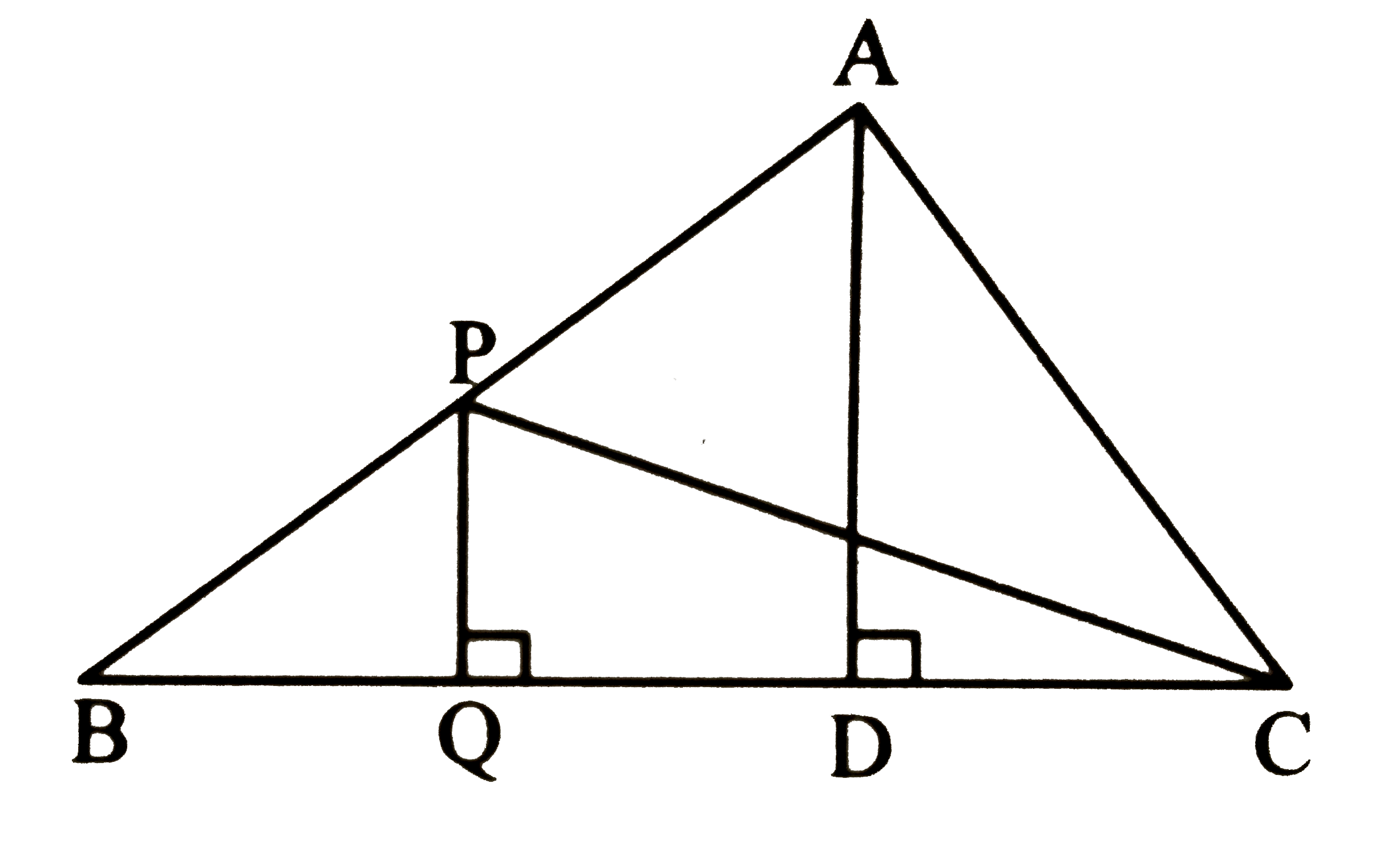
View SolutionIn the adjoining figure, then find ratio
.
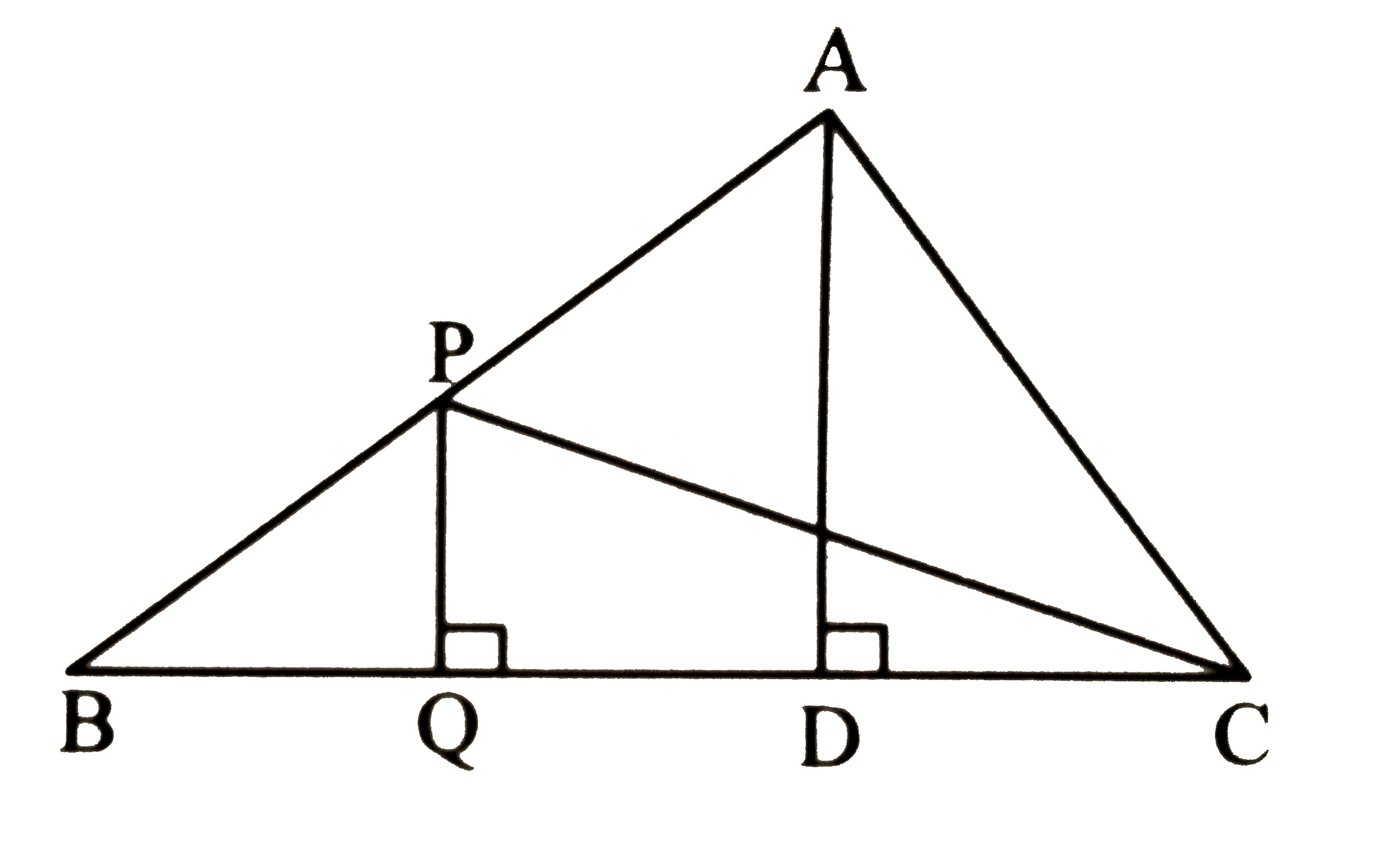
View SolutionIn the adjoining figure, then find ratio
.
View SolutionIn the adjoining figure, then find ratio
.
View SolutionIn the adjoining figure, then find ratio
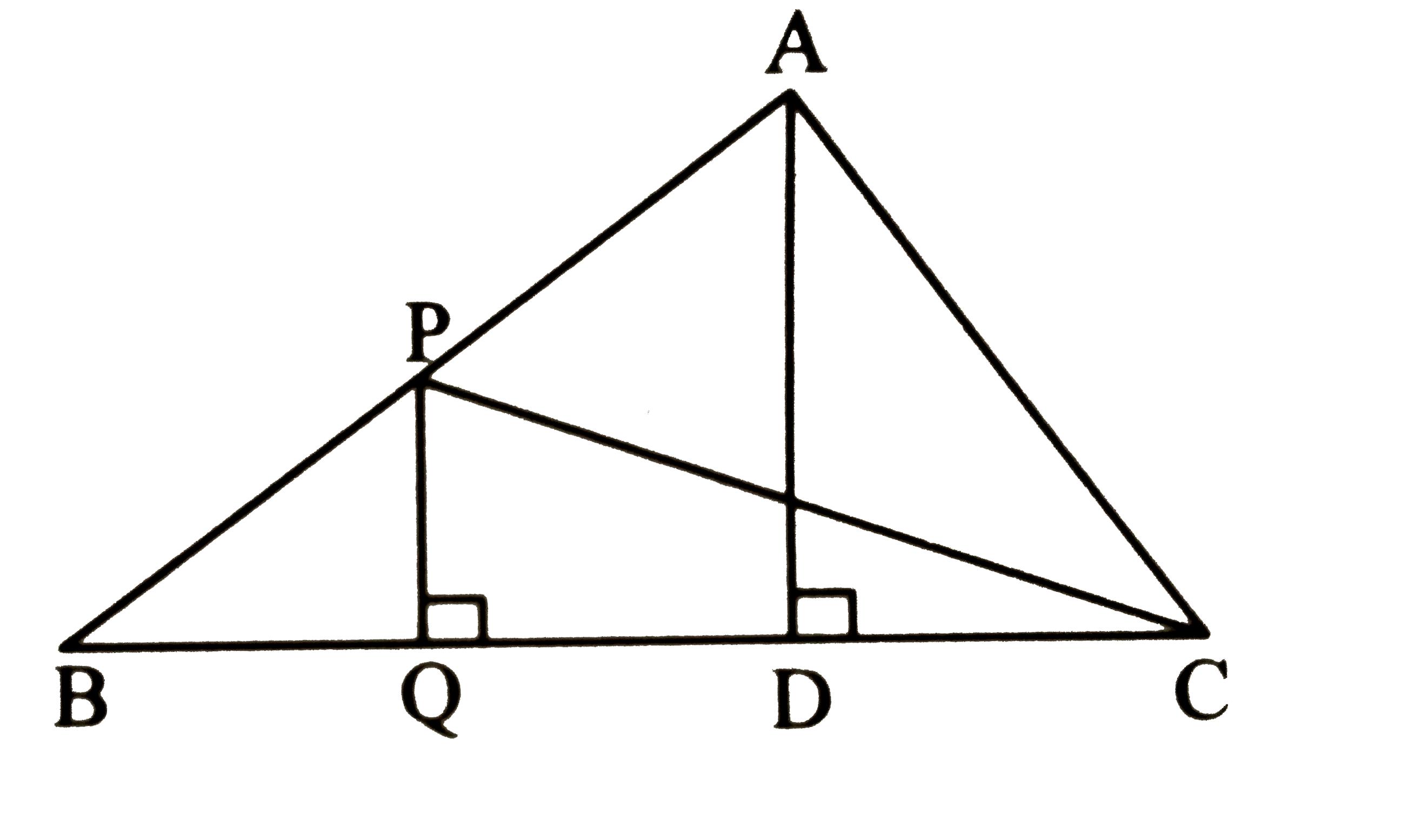
View SolutionIn the adjoining figure, then find ratio
.
View SolutionIn the adjoining figure, then find ratio
.
View SolutionIn the adjoining figure, then find ratio

View SolutionIn adjoining figure, , then find the following ratios.
View SolutionIn , AD is the median and . Prove that
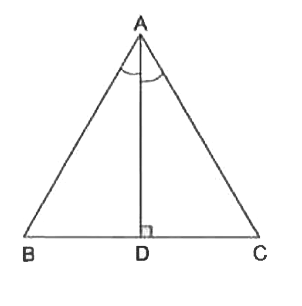
View SolutionIn the adjoining figure, ABC is a triangle in which AD is the bisector of . If , show that is isosceles.
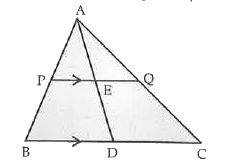
View SolutionIn a , let P and Q be points on AB and AC respectively such that . Prove that the median AD bisects PQ.
View SolutionIn the adjoining figure, ,
then find ..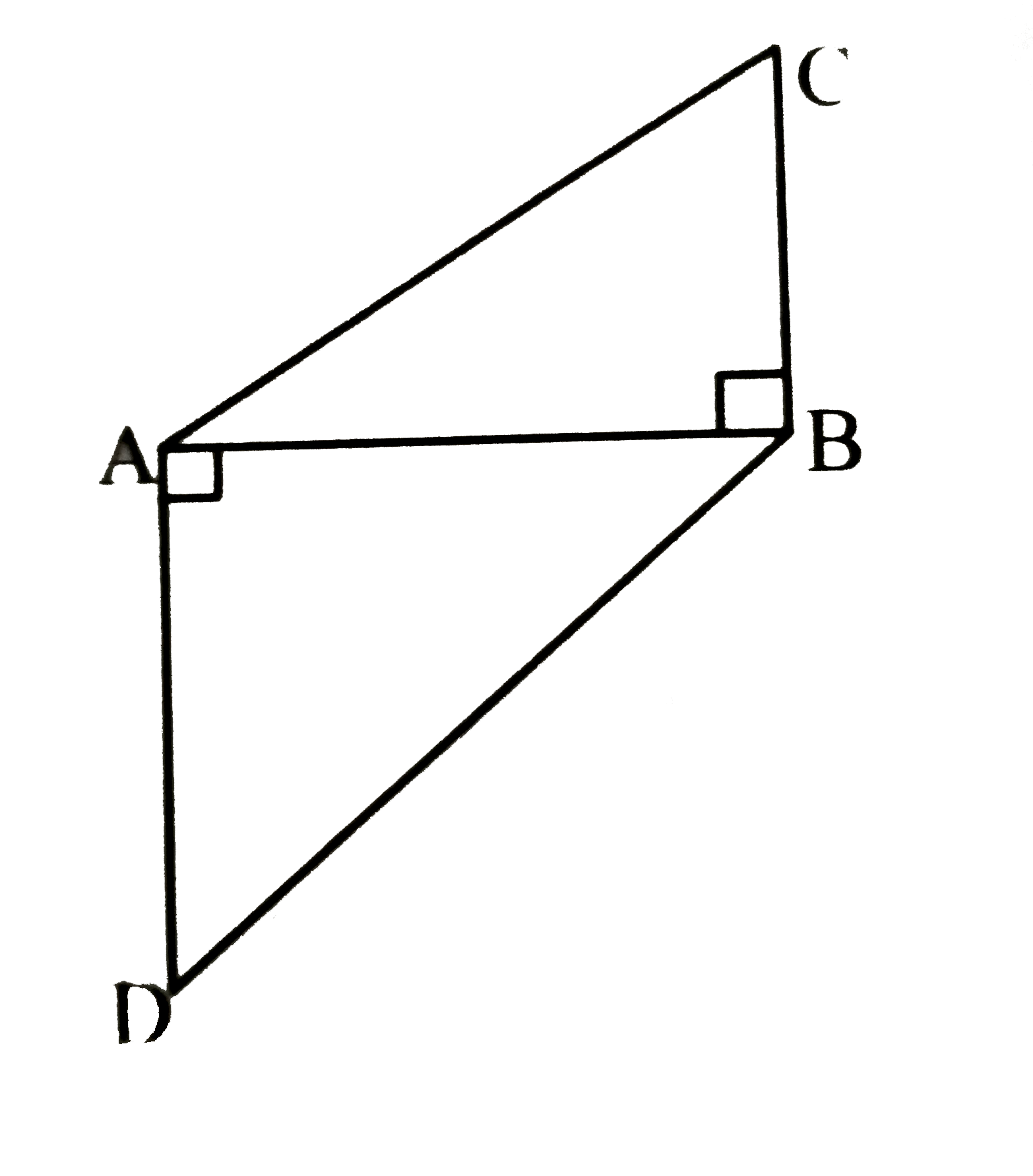
View SolutionIn the adjoining figure, then find ..

View SolutionIn /_\ ABC and /_\ PBC , AP || BC and D point on BC such that AD_|_ BC and AD = 30 cm and area(ABC) = 45cm^2 then BC=?
View Solution∆ABC ~ ∆PQR. AD is the median to BC and PM is the median to QR. Prove that AB/PQ=AD/PM
View SolutionIn the adjoining figure, ,AD||BC ,then find .
View SolutionIn adjoining figure, , ,then find Fig.
View SolutionIn the adjoining figure, is parallel to and , . What is the ratio of the area of to the area of ?
View SolutionIn triangle and AD is perpendicular to BC. If and , then the length of BC is:
View Solution