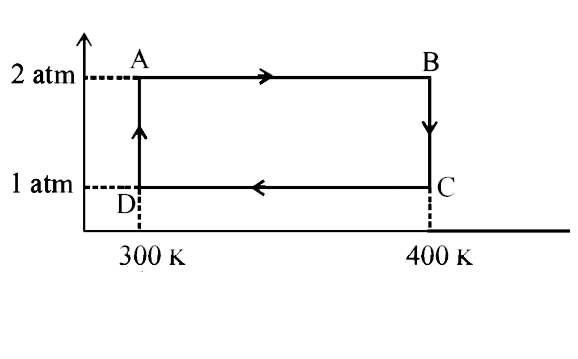
An ideal gas is made to undergo the cyclic process shown in the figure below. Let ΔW depict the work done. ΔU be the change in internal energy of the gas and Q be the heat added to the gas. Sign of each of these three quantities for the whole cycle will be 0 refers to no changeA – 0 – B + 0 + C 0 0 0 D + + +
Correct option A – 0 – Explanation:
Related Solutions
An ideal gas is made to undergo the cyclic process shown in the figure below. Let depict the work done, be the change in internal energy of the gas and be the heat added to the gas. sign of each of these three quantities for the whole cycle will be (0 refers to no change)

View SolutionAn ideal gas is taken in a cyclic process as shown in the figure. Calculate (a) work done by the gas. (b) work done on the gas (c) Net work done in the process
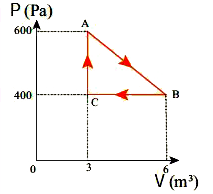
View SolutionAn ideal gas is taken in a cyclic process as shown in the figure. Calculate (a) work done by the gas. (b) work done on the gas (c ) Net work done in the process
View SolutionTwo moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal. The net work done by the gas is
View SolutionThree moles of an ideal gas undergo a cyclic process shown in figure. The work done by the gas during the process is
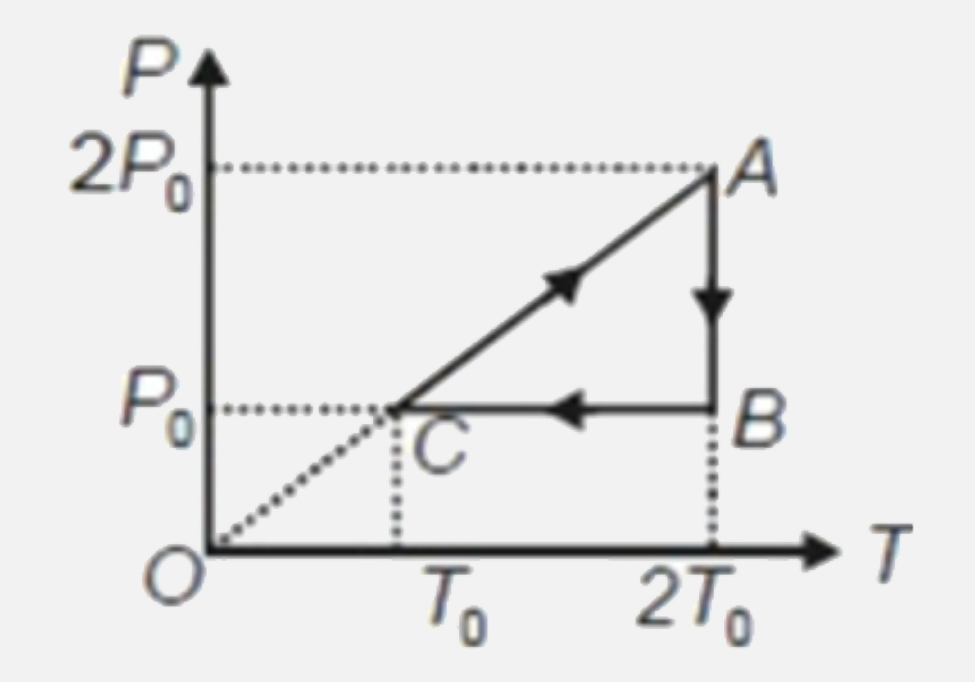
View SolutionTwo moles of an ideal monoatomic gas undergoes a cyclic process ABCA as shown in V-T diagram below: Work done by the gas during the entire cycle is :
View SolutionAn ideal gas undergoes a cyclic process whose indicator diagram is as shown in the figure. Find the work done by the gas in 1 complete cycle.
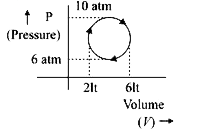
View SolutionAn ideal gas undergoes a cyclic process whose indicator diagram is as shown in the figure. Find the work done by the gas in 1 complete cycle.

View SolutionIn the figure shown below, an ideal gas is carried around the cyclic process. How much work is done in one cycle if litre?
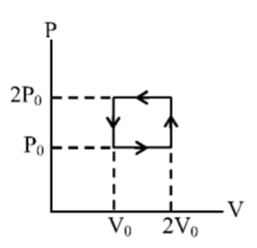
View SolutionIn the figure shown below, an ideal gas is carried around the cyclic process. How much work is done in one cycle if litre?
View SolutionOne mole of an ideal gas has an interal energy given by , where is the pressure and the volume of the gas. is a constant. This gas undergoes the quasi static cyclic process as shown in the diagram. The work done by the ideal gas in the process is

View SolutionOne mole of an ideal gas has an interal energy given by U=U_(0)+2PV , where P is the pressure and V the volume of the gas. U_(0) is a constant. This gas undergoes the quasi - static cyclic process ABCD as shown in the U-V diagram. The work done by the ideal gas in the process AB is
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process
(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process
(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy

View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process

(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process

(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process

(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from to, the work done on the gas during the process to is when the gas is taken from to the heat absorbed by the gas is Then change in internal energy of the gas in the process to is :

View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from to, the work done on the gas during the process to is when the gas is taken from to the heat absorbed by the gas is Then change in internal energy of the gas in the process to is :

View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from B to A, the work done on the gas during the process B to A is 30J, when the gas is taken from A-B the heat absorbed by the gas is 20J. The change in internal energy of the gas in the process A-B is :
View Solution