A stone is thrown straight downward with a speed of 20 m/s from the top of a tall building. If the stone strikes the ground 3.0 s later about how tall is the building? Assume air resistance is negligible. A 45 m B 60 m C 90 m D 105 m E 120 m
Correct option D 105md = vit + ½gt2
Related Solutions
A stone is thrown from the top of a building with an initial velocity of 20 m/s downward. The top of the building is 60 m above the ground. How much time elapses between the instant of release and the instant of impact with the ground ?
View SolutionA stone is thrown at a speed of from top of a building of height 25 m. Find out how far from the foot of building can the stone be thrown.
View SolutionA stone is thrown at a speed of 20 m//s from top of a building of height 25 m. Find out how far from the foot of building can the stone be thrown.
View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View SolutionA man standing on the edge of the terrace of a high rise building throws a stone, vertically up with at speed of 20 m//s . Two seconds later, an identical stone is thrown vertically downwards with the same speed of 20 m ,. Then
View SolutionA man standing on the edge of the terrace of a high rise building throws a stone, vertically up with at speed of 20 m//s . Two seconds later, an identical stone is thrown vertically downwards with the same speed of 20 m ,. Then
View SolutionA stone is dropped from the top of a tall cliff and n seconds later another stone is thrown vertically downwards with a velocity u m/s. How far below the top of the cliff the second stone will overtake the first?
View SolutionFrom the top of a building 30 m tall, the angle of depression of the object on the ground is . How far is the object from the buildings?
View SolutionA body thrown horizontally from the top of a building with a speed , strikes the ground away from the foot of tower. The height of the tower is
View SolutionA stone is thrown horizontally with a velocity of 15 m/s from the top of a building 19.6 m high. Find the distance from the foot of the building where it strikes the ground.
View Solutionഒരു കെട്ടിടത്തിന് മുകളിൽ നിന്ന് താഴേക്കിട്ട കല്ല് തറയിൽ പതിക്കാൻ 3 സെക്കൻഡ് വേണ്ടിവന്നു. എങ്കിൽ കെട്ടിടത്തിന്റെ ഉയരം എത്ര?
View SolutionTwo tall buildings are 40 m apart. With what speed should a ball be thrown horizontally from a window in a building 145 m above the ground, so that it enters a window in another building 22.5 m above the ground?
View SolutionA ball is thrown downwards with a speed of , from the top of a building high and simultaneously another ball is thrown vertically upwards with a speed of from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
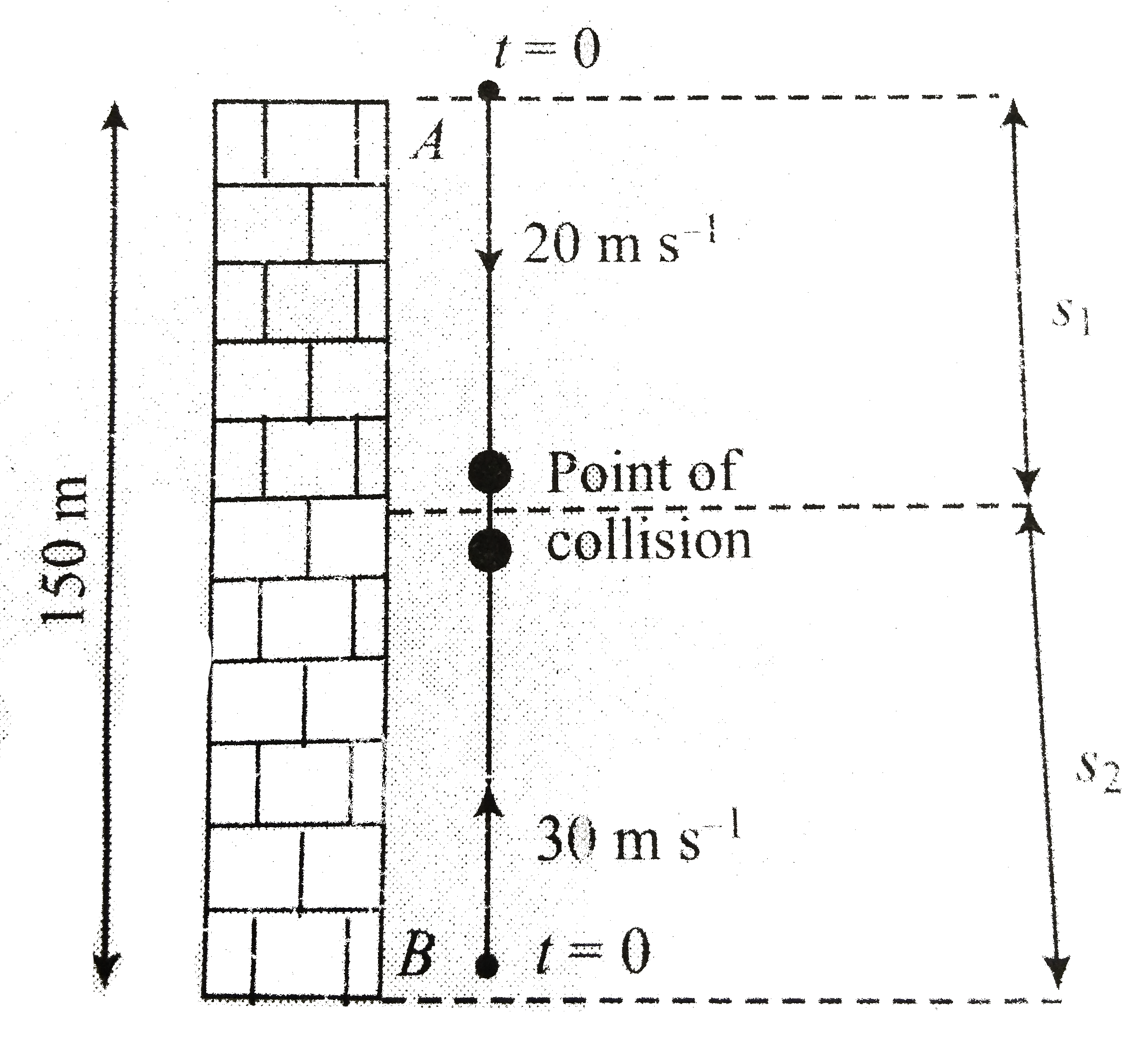 .
.
View SolutionA stone is released from top of a building of height h. When it goes by 5 m from top then at this 25 m below the top of the building. Both the stones reached the ground simultaneously. Find height h of the building.
View SolutionA ball is thrown upward from the top of a 25.0 m tall building. The ball's initial speed is 12.0 m/s. At the same instant, a person is running on the ground at a distance of 31.0 m from the building. What must be the average speed of the person if he is to catch the ball at the bottom of the building ?
View SolutionTwo tall buildings are 100 m apart with what speed must a ball be thrown horizontally from the window 500 m above the ground in one building. So that it will enter a window 100 m above the ground in the other ?
View SolutionA ball is thrown from the top of a building with a velocity of 10 m/s and returns with a velocity of 30 m/s to the ground. Find the height of the building.
View SolutionA stone falls from a building and reaches the ground 2.5 seconds later. How high is the building?
View SolutionA stone is shot straight upward with a speed of 20 m/s from a tower 200 m high. The speed with which it strikes the ground is (g=10 m/s^2)
View Solution