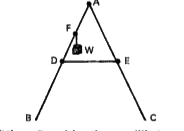
As shown in Fig.7.40 the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE 0.5 m is tied half way up. A weight 40 kg is suspended from a point F 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder find the tension in the rope and forces exerted by the floor on the ladder. Take g = 9.8 m/s2
The given situation can be shown as:NB = Force exerted on the ladder by the floor point BNC = Force exerted on the ladder by the floor point CT = Tension in the ropeBA = CA = 1.6 mDE = 0. 5 mBF = 1.2 mMass of the weight m = 40 kgDraw a perpendicular from A on the floor BC. This intersects DE at mid-point H.ΔABI and ΔAIC are similarBI = ICHence Iis the mid-point of BC.DE || BCBC = 2 x DE = 1 m AF =BA – BF = 0.4 m … iD is the mid-point of AB.Hence we can write:AD=1/2xBA=0.8m................iiUsing equations i and ii we get:FE = 0.4 mHence F is the mid-point of AD.FG||DH and F is the mid-point ofAD. Hence G will also be the mid-point of AH.ΔAFG and ΔADH are similarFor translational equilibrium of the ladder the upward force should be equal to the downward force.Nc + NB = mg = 392 … iiiFor rotational equilibrium of the ladder the net moment about A is:NC=245 NNB=147 NFor rotational equilibrium of the side AB consider the moment about A.
Related Solutions
As shown in Fig.7.40, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take )
View SolutionAs shown in Fig.7.40, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take )
View SolutionAs shown in Fig.7.40, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m//s^(2) )
View SolutionAs shown in Fig.7.40, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m//s^(2) )
View SolutionAs shown in Fig. the two sides of a step ladder BA and CA are 1.6 m long and hinged at A . A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA . Assuming the floor to be fricionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m//s^(2)) (Hint. Consider the eqilibrium of each side of the ladder separately.)
View SolutionAs shown in fig. the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F.1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder
(Take )
View SolutionAs shown in the given figure. the two sides of a step ladder BA and CA are 1.6 m long and hinged at A.A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1,2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in te rope and forces exerted by the floor on the ladder. (Take g = 9.8 ms^-2 ) (Hint: consider the equilibrium of each side of the ladder separately).
View Solutionसलग्न चित्र में दिखाया गया है की एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1 .6 मीटर है और इनको A पर कब्ज़ा लगा कर जोड़ा गया है| इन्हे ठीक बिच में 0 .5 मीटर लम्बी रस्सी DE द्वारा बाँधा गया है| सीढ़ी BA के अनुदिश B से 1 .2 मीटर की दुरी पर स्थित बिंदु F से 40 किग्रा का एक भार लटकाया गया है|यह मानते हुए की फर्श घर्षणरहित है और सीढ़ी का भार उपेक्षणीय है, रस्सी में तनाव और सीढ़ी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए|
मीटर /सेकंड लीजिए)
View Solutionजैसा चित्र 7 ।40 में दिखाया गया है, एक खड़ी होने वाली सीढी के दो पक्षो BA और CA की लम्बाई है और इनको A पर कब्जा लगा कर जोड़ा गया है । इन्हे ठीक बीच में 0.50 M लम्बी रस्सी DE द्वारा बांधा गया है । सीढी BA के अनुदिश b से 1.2m की दूरी पर स्थित बिंदु F से 40 kg का एक भार लटकाया गया है । यह मानते हुए कि फर्श घर्षण रहित है और सीढी का भार उपेक्षणीय है , रस्सी में तनाव और सीढी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए (लीजिए )

View Solutionजैसा चित्र में दिखाया गया है, एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्ज़ा लगा कर जोड़ा गया है । इन्हें ठीक बीच में 0.5m लंबी रस्सी DE द्वारा बाँधा गया है । सीढ़ी BA के अनुदिश B से 1.2m की दूरी पर स्थित बिंदु F से 40kg का एक भार लटकाया गया है । यह मानते हुए कि फर्श घर्षण रहित है और सीढ़ी का भार उपेक्षणीय है, रस्सी में तनाव और सीढ़ी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए । (लीजिए )
[संकेत : सीढ़ी के दोनों ओर के संतुलन पर अलग-अलग विचार कीजिए )
View Solutionजैसा चित्र में दिखया गया है, एक खड़ी होने वाली सीढ़ी की दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्जा लगा कर जोड़ा गया है | इन्हें ठीक बीच में 0.5m लम्बी रस्सी DE द्वारा बांधा गया है | सीढ़ी BA के अनुदिश B से 1.2 m की दूरी पर स्थित बिंदु F से 40 kg का एक भार लटकाया गया है | यह मानते हुए की फर्श घर्षण रहित पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए ( लीजिए )
संकेत के दोनों और के संतुलन पर अलग अलग विचार कीजिए
View SolutionThe step-ladder shown in figure 6.11 is 8 m long and hinged at C.BD is a tie rod 2.5 m long half way up. A man of 86 kg climbs 6 m along the ladder . Find the tension in the tie rod the forces exerted on the ladder by the assuming the floor to frictionless and the ladder weightless. [Hints: Consider the free-body diagram of the sides of the ladder.]
View SolutionA ladder 3.7 m long is placed against a wall in such a way that the foot of the ladder is 1.2 m away from the wall. Find the height of the wall to which the ladder reaches.
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View Solutiona 17 m. The long ladder rests on a vertical wall in such a way that the foot of the ladder is 8 m from the foot of the wall. Is at a distance of. If the top of the ladder is 2 m. slip, the foot of the ladder will almost slip
View Solution5.5 मी लंबी एक सीढ़ी एक दीवार के सहारे टिकी हुई है। यह सीढ़ी दीवार की 4.4 मी ऊंचाई तक पहुँचती है। सीढ़ी के निचले सिरे की दीवारे से दूरी तय कीजिए।
View Solution25 मी लम्बी एक सीढ़ी एक बिल्डिंग की 20 मीटर ऊँची खिड़की तक पहुँचती है सीढ़ी के पाद की बिल्डिंग से दूरी ज्ञात कीजिये
View SolutionA 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet reston the floor 1 m from the wall as shown in fig. Find the reaction forces of the wall and the floor.
View SolutionA 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.
View Solution