Twelve capacitors each having a capacitance C are connected to form a cube. Find the equivalent capacitance between the diagonally opposite corners such as A and B.
Applying the Kirchoff’s second law across diagonal points A and B to find the charge distribution across the branch of the circuit and find the equivalent capacitance.Suppose the points A and B are connected to a battey. The charges appearing on some of the capacitors are shown in figure suppose the positive terminal of the battery supplies a charge +Q through the point A. This charge is divided on the three plates connected to A. Looking from A the three sides of the cube have identical properties and hence the charge will be equally distributed on the three plates. Each of the capacitors a b and c will receive a charge Q/3. The negative terminal of the battey supplies a charge –Q through the point B. This is again divided equally on the three plates connected to B. Each of the capacitors d e and f gets equal charge Q/3.Now consider the capacitors g and h. As the three plates connected to the point E form an isolated system their total charge must be zero. The negative plate of the capacitor has a charge -Q/3. The two plates of g and h connected to E should have a total charge Q/3. By symmetry these two plates should have equal charges and hence each of these has a charge Q/6. The capacitors a g and d have charges Q/3 Q/6 and Q/3 respectively.
Related Solutions
Twelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

View SolutionFigure shows a combination of twelve capacitors each of capacitance C forming a cube . Find the equivalent capacitance of the combination ( a) between the diagonally opposite corners A and B of cube ( b) between the diagonally opposite corners A and D of a face of the cube .
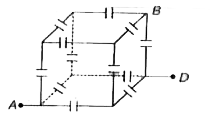
View SolutionFigure shows a combination of twelve capacitors, each pf capacitance C, forming a cube. Find the equivalent capacitance of the combination (i) between the diagonally opposite corners A and B of the cube (ii) between the diagonally opposite corners A and D of a face of the cube.
View SolutionTwelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the edges.
View SolutionTwelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the face diagonals.
View SolutionTwelve wires, each of resistance are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View SolutionFind the equivalent capacitance between and . All the capacitors have capacitance .
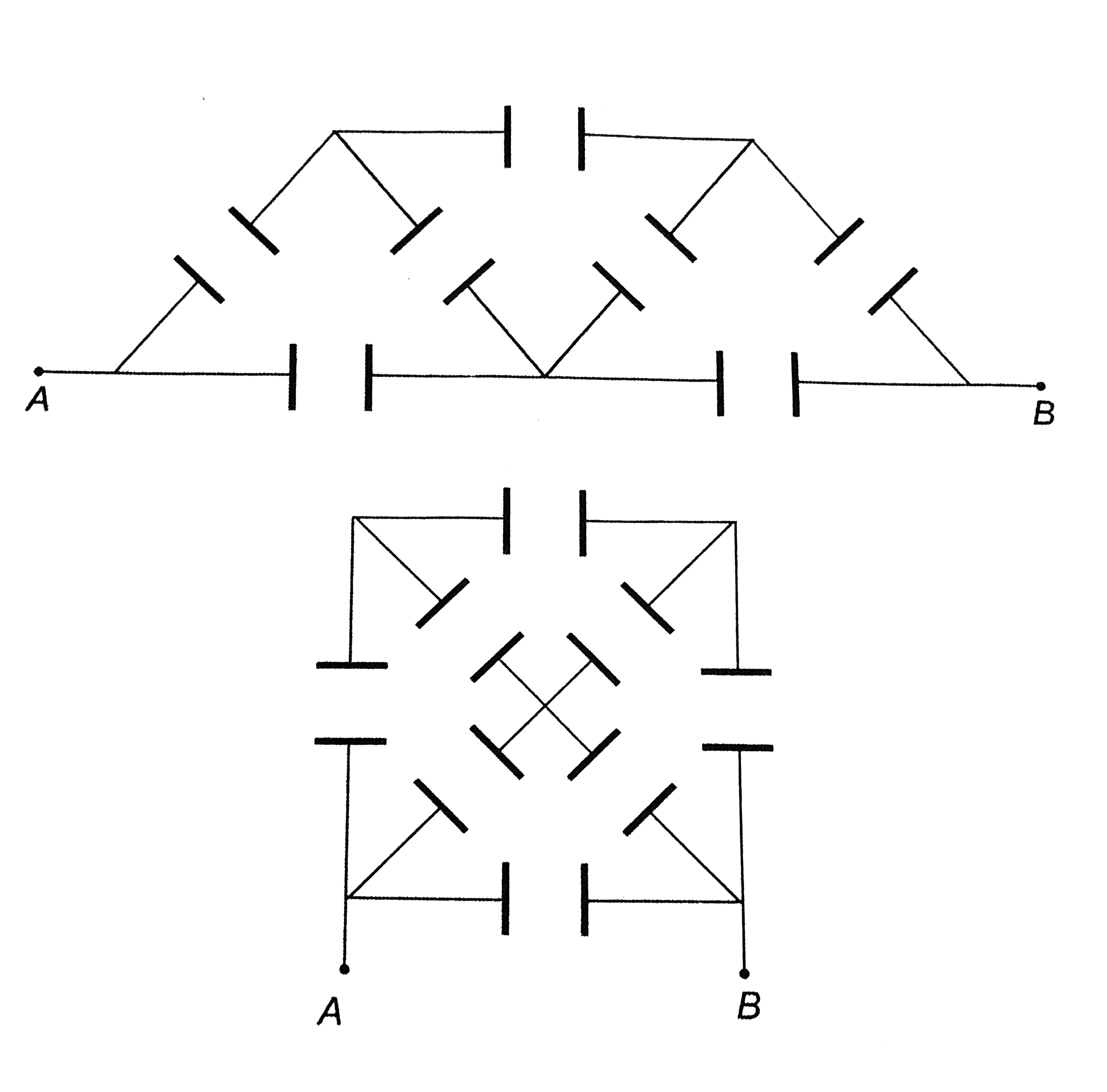
View SolutionFind the equivalent capacitance between A and B. All the capacitors have capacitance C.
View SolutionFind the equivalent capacitance between A and B. All the capacitors have capacitance C.

View SolutionTwelve equal capacitors are joined to form a cube. Find the equivalen capacitance between two opposite edges on the same plane?
View SolutionTwelve capacitors, each having capacitors, C , are joined to from a cube as shown. Find the equivalent capacitance between the ends of (a) Digitonal i.e., between A and B . (b) Face diagonal i.e., between A and C . (c) side of cube i.e., between A and D .
View SolutionFind the equivalent capacitance between terminals A & C , if each capacitor is of capacitance 4muF
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2muF .
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2muF .
View Solutionचित्र में प्रत्येक संधारित्र की धारिता है। A व B के मध्य तुल्य धारिता ज्ञात कीजिये।
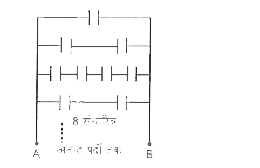
View SolutionIf each capacitor has capacitance C, then equivalent capacitance between A and B is
View SolutionIf each capacitor has capacitance C, then equivalent capacitance between A and B is
View Solution4.Three capacitors each of capacitance C are connected in series.Their equivalent capacitance will be ....................
View Solution