Let Γ be a circle with centre O. Let A be the another circle passing through O and intersecting Γ at points A and B. A diameter CD of Γ intersects A at point P different from O. Prove that ∠APC = ∠BPD.
Suppose that A is a point on A such that ∠APC = ∠BPD. Then the segments OA and OB subtends same angle in the respective minor arcs so OA = OB. This shows that A lies on Γ and hence A =A.This proves that ∠APC = ∠BPD.
Related Solutions
In two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
View SolutionP is any point on diameter of a circle with centre O.A perpendicular drawn on diameter at the point O intersects the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R.A tangent drawn at the point R intersects extended OP at the point S. Prove theat
View SolutionTwo chords AB and CD of a circle with centre O intersect at point P within the circle.
View SolutionTwo circle with centre O and P intersect each other in point C and D. Chord AB of the circle with centre O touches the circle with circle with centre P in Point E. Prove that
View SolutionThe locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
View SolutionThe locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
View SolutionTwo circles whose centres are and intersect at Through a line parallel to intersecting the circles at is drawn. Prove that
View SolutionTwo circles whose centres are and intersect at Through a line parallel to intersecting the circles at is drawn. Prove that
View SolutionIf a line intersects two concentric circles (circles with the same centre) with centre O at A,B,C and D), prove that

View SolutionIf a line intersects two concentric circles ( circles with the same centre ) with centre O at A, B, C and D, prove that AB = CD.
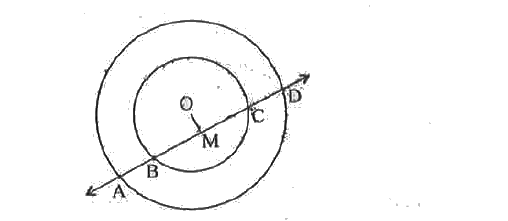
View SolutionIf a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD
View SolutionIf a line intersects two concentric circles (circles with the same centre) with centre O at A,B,C and D, prove that AB = CD
View SolutionO is a point P on a diameter of a central circle. Intersect the perpendicular circle drawn at point O on that diameter at point Q. The extended QP intersects the circle at the point R. The tangent drawn at point R intersects the extended OP at point S. Prove that SP = SR.
View SolutionP is a point outside a circle with centre O, and it is 14 cm away from the centre. A secant PAB drawn from P intersects the circle at the points A and B such that PA = 10 cm and PB = 16 cm. The diameter of the Circle is:
View SolutionIn the center circle O AB is a diameter and AC is a chord. A straight line passing through point O parallel to AC intersects the pressure BC at point D. Prove that BD = CD
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.
Prove that:
View Solutioncosαsin(β−γ)+cosβsin(γ−α)+cosγsin(α−β)=
View SolutionLet A be one point of intersection of two intersecting circles with centres O and Qd . The tangents at A to the two circles meet the circles again at B and C respectively. Let the point P be located so that AOPQ is a parallelogram. Prove that P is the circumcentre of the triangle ABC.
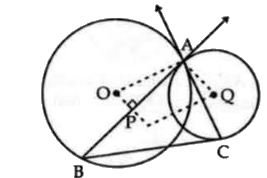
View SolutionTA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
View SolutionTwo cocentric circle common centre O. A line 'l' intersects these circle A,B,C and D. Prove that AB = CD.
View Solution