Let ABC be an acute-angled triangle and let D E F be the feet of the perpendiculars from A B C respectively to BC CA AB. Let the perpendiculars from F to CB CA AD BE meet them in P Q M N respectively .Prove that P Q M N are collinear.
Explanation:Observe that C Q F P or concyclic. Hence∠CQP = ∠CQP= 90° - ∠FCP = ∠B Similarly the concyclicity of F M.Q A gives ∠AQN = 90° + ∠FQM = 90° + ∠FAM = 90° + 90° - ∠B =180° - ∠B. Thus we obtain ∠CQP + ∠AQN = 180° . It follows that Q N P lie on the same line.We can similarly prove that ∠CPQ + ∠BPM = 180° . This implies that P M Q are collinear. Thus M N both lie on line joining P and Q.
Related Solutions
Let and be the vertices of triangle and let and be the feet of the perpendiculars drawn from onto the sides and respectively then
View SolutionABC is a right angled triangle which is right angled at C. Let AB=c, BC=a, CA=b and let p be the length of perpendicular from C and AB. Prove that .
View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
View SolutionD,E,F are the foot of the perpendiculars from vertices A,B,C to sides BC,CA,AB respectively,and H is the or the centre of acute angled triangle ABC, where a,b,c are the sides of triangle ABC, then
View SolutionABC is a right Triangle right angled at C. Let BC=a,CA=b,AB=c and let p be the length of the perpendicular fromt C on AB Prove that.
View SolutionFor triangle ABC, R = 5/2 and r=1. Let be the incenter of the triangle and be the feet of the perpendiculars from to , respectively. The value of is equal to
View SolutionABC is right angle triangle at C. Let BC=a ,CA=b,AB=c and Let 'P' be the length of perpendicular from C to AB.prove that (1)/(p^(2))=(1)/(a^(2))+(1)/(b^(2))
View SolutionIn a . Feet of the perpendicular from A, B and on the opposite sides BC, CA and AB are D, E and F respectively and perpendiculars are concurrerant at P.
Now match the entries of Column-I with respective entries of column-II.
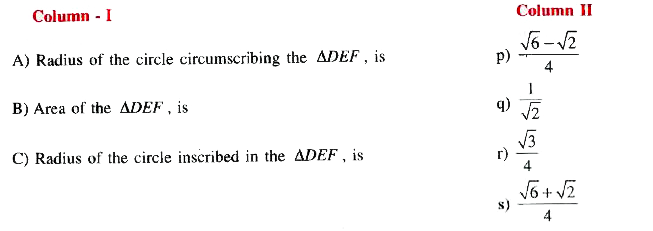
View SolutionFor a triangle . Let D, E and F be the feet of the perpendiculars from incentre I to BC, CA and AB, respectively. Then the value of is equal to _____
View SolutionFor a triangle . Let D, E and F be the feet of the perpendiculars from incentre I to BC, CA and AB, respectively. Then the value of is equal to _____
View SolutionFor a triangle ABC, R = (5)/(2) and r = 1 . Let D, E and F be the feet of the perpendiculars from incentre I to BC, CA and AB, respectively. Then the value of ((IA) (IB)(IC))/((ID)(IE)(IF)) is equal to _____
View SolutionABC is a right Triangle right angled at C. Let BC=a,CA=b,AB=c and let p be the length of the perpendicular fromt C on AB Prove that pc=ab
View Solutionis a triangle where and let 'p' be the length of the perpendicular from C on AB. Prove that:
View SolutionLet ABC be a triangle with incentre at I. Also, let P and Q be the feet of perpendiculars from A to BI and CI, respectively. Then which of the following result are correct?
View SolutionLet P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then angle A equals -
View SolutionLet P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then angle A equals -
View SolutionLet P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then angle A equals -
View SolutionIn a , let P and Q be points on AB and AC respectively such that . Prove that the median AD bisects PQ.
View SolutionIf P,Q and R are the mid-point of the side BC,CA and AB of a triangle and AD is the perpendicular form A and BC, prove that P,Q and D are concylic.
View SolutionConsider Let I be the incentre and a,b c be the sides of the triangle opposite to the angle A,B,C respectively. Let O be any point in the plane of within the triangle . AO ,BO ,CO meet the sides BC, CA and AB in D, E and F respectively then
View Solution