Let ABCD be a convex quadrilateral P Q R S be the mid points of AB BC CD DA respectively such that triangles AQR and CSP are equilateral. Prove that ABCD is a Rhombus. Determine its angles.
Explanation:We have QR = BD/2 = PS. Since AQR and CSP are both equilateral and QR = PS They must be congruent triangles. This implies that AQ = QR = RA = CS = SP = PC. Also ∠CEF=60°=∠RQA. Fig. 1Hence CS is parallel to QA. Now CS = QA implies that CSQA is a parallelogram. In particular SA is parallel to CQ and SA = CQ. This shows that AD is parallel to BC and AD = BC. Hence ABCD is a parallelogram. Let the diagonal AC and BD bisect each other at W. Then DW = DB/2 = QR = CS = AR. Thus in triangle ADC the medians AR DW CS are all equal. Thus ADC is equilateral. This implies ABCD is Rhombus. Moreover the angle are 60°and 120°.
Related Solutions
ABCD एक समचतुर्भुज है। AB,BC,CD,DA के मध्य-बिंदु क्रमशः P,Q,R,S हैं। सिद्ध कीजिए कि PQRS एक आयत है।
View SolutionABCD is a rectangle and P,R and S are the mid - points of the AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
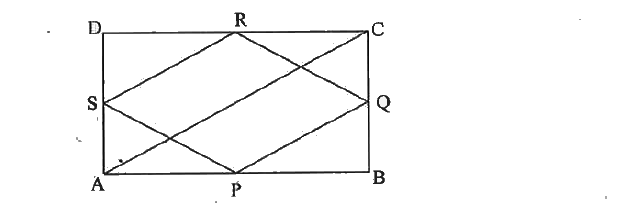
View SolutionABCD is a rectangle and P,Q,R and S are the mid points of the sides AB,BC,CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View SolutionABCD is a rhombus and are the mid-points of respectively. Prove that is a rectangle.
View SolutionIn quadrilateral ABCD if P,Q,R,S are mid-point of AB,BC,CD,DA resp. then SR is parallel to
View SolutionIn quadrilateral ABCD if P,Q,R,S are mid-point of AB,BC,CD,DA resp. then which of the following is true?
View SolutionLet ABCD be a rectangle. If the mid-points of the sides AB, BC, CD, DA are respectively P, Q, R, S, then what is the quadrilateral PQRS?
View SolutionP,Q,R and S are respectively the mid points of the sides AB,BC,CD and DA of a quadrilateral ABCD such that ACbotBD . Prove that PQRs is a rectangle.
View Solution