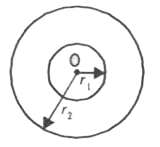
Space between two concentric conducting spheres of radii a and b b > a is filled with a medium of resistivity p .The resistance between the two spheres will be :1 p/2π 1/a + 1/b2 p/4π1/a + 1/b3 p/2π1/a - 1/b3 p/4π1/a - 1/b
Correct option 4 p/4π 1/a - 1/bExplanation:Resistance of spherical shell is R = p/4π[b-a/ab]
Related Solutions
The space between two concentric spheres of radii , and t. is filled with a material of resistivity p. The resistance between inner and outer surface is :
View SolutionFor two events A and B,P(A)=1/3=1-P(B) and P(B/A)=1/4
Find P(A/B)
View SolutionFill in the Blanks :
A and B are two events such that P(A) = 1/2, P(B) = 1/3, P(A B) = 1/4, then P(A/B) =..
View SolutionIf A and B are two events such that , then is
View SolutionIf A and B are two events such that P(A) = P(B) = 1, then show that ,
P(A+B) = 1, P(AB) = 1
View SolutionIf A and B are two events such that then P ( not A and not B) =
View SolutionFor two events A and B,P(A)=1/3=1-P(B) and P(B/A)=1/4
Find P(AB) and P(B)
View SolutionTwo events and are such that and then
View SolutionThere are two concentric spheres of radius (a) and (b) respectively. If the space between them is filled with medium of resistivity , then the resistance of the intergap between the two spheres will be
View SolutionThere are two concentric spheres of radius a and b respectively. If the space between them is filled with medium of resistivity rho , then the resistance of the intergap between the two spheres will be (Assume bgta )
View Solutionযদি ও দুটি ঘটনা এবং হয়, তবে প্রমাণ করো যে, তারপর দেখাও যে,
View SolutionIf A and B are two events and , prove that,
Hence, deduce that, .
View SolutionA' and 'B' are two events such that 'P(A)=1/4, P(A / B)=(1/3)' and 'P(B / A)=1/2', find 'P(B)' and 'P(A / barB)'
View SolutionIf A and B are two events such that P((A B)')= and P(A')=, then P(A) and P(B) are
View SolutionIf A and B are two events such that and then find
View SolutionIf A and B are two events such that ,, then find,
View SolutionA and B are two events such that , then P(B)= ………….
View SolutionIf A and B are two events such that and . Find :
(i) (ii) (ii) (iv)
View SolutionIf A and B are two events and P(B)!=1 prove that,P[(A)/(B^(c))]=(P(A)-(P(A nn B)))/(1-P(B)) Hence,deduce that.P(A nn B)>P(A)+P(B)-1
View SolutionIf A and B are two events of a random experiment such that P(A) = (1)/(4), P(B) = (1)/(2)P(A and B)=(1)/(8) then find i. P(A or B) ii. P (not A and not B). iii. P(A and not B), P(not A and B)
View Solution