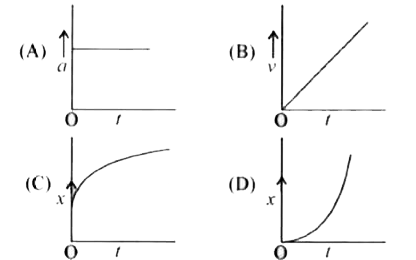
A particle starts from origin O from rest and moves with a uniform acceleration along the positive x-axis. Identify all figures that correctly represent the motion qualitatively. a = acceleration v = velocity x = displacement t = time1 A 2 A B D 3 B C 4 A B C
Correct option 2Explanation:
Related Solutions
A particle starts from origin O from rest and moves with a uniform acceleration along the positive x=axis. Identify all figures that correctly represent the motion qualitatively. (a=acceleration , v=velocity, x=displacement,t=time)
View Solutionएक कण स्थिरावस्था से एक धनात्मक x-अक्ष की दिशा में मूल बिंदु O से नियत त्वरण से चलता है | वह सभी चित्र ज्ञात कीजिये जो इस कण की गति को गुणात्मक रूप से सही दर्शाते हैं (a = त्वरण, v = वेग, x = विस्थापन, t = समय)
View SolutionA particle starts from origin with uniform acceleration. Its displacement after t seconds is given in meter by the relation x=2+5t+7t^2 . Calculate the magnitude of its a. Initial velocity b. Velocity at t=4s c. Uniform acceleration d. Displacement at t=5s
View SolutionA particle starts from origin with uniform acceleration. Its displacement after t seconds is given in meter by the relation . Calculate the magnitude of its
a. Initial velocity
b. Velocity at
c. Uniform acceleration
d. Displacement at
View SolutionA particle is moving under constant acceleration . The motion starts from rest. The velocity and displacement as a function of time t is
View SolutionA particle moves along the X-axis as x=u(t-2)+a(t-2)^(2) a) the initial velocity of the particle is u b) the acceleration of the particle is 2a c) at t=2s particle is at the origin
View SolutionA particle moves along the X-axis as
a) the initial velocity of the particle is u
b) the acceleration of the particle is 2a
c) at particle is at the origin
View SolutionIf acceleration gradient of a moving body along positive x-axis is -4s^(-2) and body starts its motion from rest from x = 5m , having maximum acceleration (magnitude) then velocity of moving body at x = -3m is
View SolutionIf acceleration gradient of a moving body along positive x-axis is -4s^(-2) and body starts its motion from rest from x = 5m , having maximum acceleration (magnitude) then velocity of moving body at x = -3m is
View SolutionRepresent graphically the motion of a body starting from rest and moving with uniform acceleration both in terms of velocity-time and displacement -time.
View Solutionx-coordinate of a particle moving along this axis is Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at
View Solutionx-coordinate of a particle moving along this axis is x = (2+t^2 + 2t^3). Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at t=2s.
View SolutionA particle moves with constant acceleration a in the positive x-axis. At the particle is at origin is at rest , then correct graph between and displacement is :
View SolutionA particle moves with constnat acceleration in the positive x-axis. At the particle is at and is at rest, then correct grahp between velocity and displacement is:
View SolutionVelocity time graphs of particles and moving along -axis are shown here. Both and start from origin:

View SolutionVelocity time graphs of particles and moving along -axis are shown here. Both and start from origin:

View SolutionDisplacement-time equation of a particle moving along x-axis is (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
View SolutionDisplacement-time equation of a particle moving along x-axis is (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
View SolutionDisplacement-time equation of a particle moving along x-axis is (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
View SolutionDisplacement (x) of a particle is related to time (t) as x = at + b t^(2) - c t^(3) where a,b and c are constant of the motion. The velocity of the particle when its acceleration is zero is given by:
View Solution