A magnetic field vector B = Bo j exists in the region a < x < 2a and B = – B0J˄ in the region 2a < x < 3a where Bo is a positive constant. A positive point charge moving with a velocity V = Vo ↑ where Vo is a positive constant enters the magnetic field at x = a. The trajectory of the charge in this region can be like
The correct option Explanation:Force experienced by charge q is F = qV × BIn the region x = a to x = 2a F1 = qV0i × B0j = qV0B0k…..i × j = kF1 is along positive z axis.In the region x = 2a to 3a F2 = qV0i × – B0j = – qV0B0kF2 is directed along negative z axis∵ F1 & F2 are perpendicular to velocity V.
Related Solutions
A magnetic field vec B = B_0 hat j exists in the region a lt x lt 2a and vec B = - B_(0) hat i in the region 2a lt x lt 3a , where B_0 is positive constant. A positive point charge moving with a velocity vec v = v_0 hat i where v_0 is a positive constant, enters. the magnetic field at x=a, The trajectory of the charge in this region can be like,
View SolutionA magnetic field B=B_(0)hatj exists in the region a lt x lt 2a and B=-B_(0)hatj , in the region 2a lt x lt 3a , where B_(0) is a positive constant. A positive point charge moving with as velocity v=v_(0)hati , where v_(0) is a positive constant, enters the magnetic field at x=a , the trajectory of the charge in this region can be like:
View SolutionA magnetic field , exists in the region , and vec(B) = -B_(0) hat(j)2a lt xlt 3aB_(0)vec(v) = v_(0) hat (i)v_(0) is a positive constant , enters the magnetic field at . The trajectory of the charge in this region can be like

View SolutionA magnetic field , exists in the region , and , in the region , where is a positive constant . A positive point charge moving with a velocity , where is a positive constant , enters the magnetic field at . The trajectory of the charge in this region can be like

View SolutionA magnetic field exists in the region , in the region , where is a positive constant. A positive point charge moving with a velocity , where is a positive constant, enters the magnetic field atx=a. The trajectory of the charge in this region can be like.
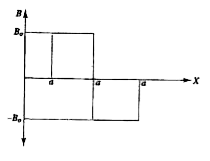
View SolutionMagnetic field vec(B)=B_(0)hatj , Campus a lt x lt 2a In and vec(B)=-B_(0)hatj Campus 2a lt x lt 3a Is present in B_(0) Is a positive constant. A positive point charge vec(V)=V_(0)hati Is moving from Where V_(@) Is a positive constant. It enters the magnetic field at x = a. The projected path of charge in this region will be
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines Beyond the line (i.e., in the region ), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line .
b. the pitch of the helix formed after the particle enters the region (Mass of the particle is m.)
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0 and x=a. Beyond the line x=a (i.e., in the region xgta ), there exists a magnetic field of strength B, directed along the positive y-axis. Find a. at which point does the particle meet the line x=a . b. the pitch of the helix formed after the particle enters the region xgea. (Mass of the particle is m.)
View SolutionA positively charged particle is moving along the positive x-axis in a unifom electric field and magnetic field (where and are positive constants), then
View SolutionA positively charged particle B hat j In the magnetic field of value v hat k Enters with velocity. Particle will run
View SolutionA particle of mass m and charge q moving with constant velocity v along positive x direction enters a region containing a uniform magnetic fileld B directed along the negative z direction, extending from x = a to x = b. For the particle to enter the region x gt b , the minimum value of v is
View SolutionA charge q moves in a region, where electric field and magnetic field both exist, then the force on it is
View Solutionक्षेत्र में चुंबकीय क्षेत्र है तथा क्षेत्र में चुंबकीय क्षेत्र है, जहाँ धनात्मक अचर है। वेग जहाँ धनात्मक अचर है, से चलता हुआ एक धनात्मक बिंदु-आवेश चुंबकीय क्षेत्र में पर प्रवेश करता है। इस क्षेत्र में आवेश के पथ का सही निरूपण हो सकता है :
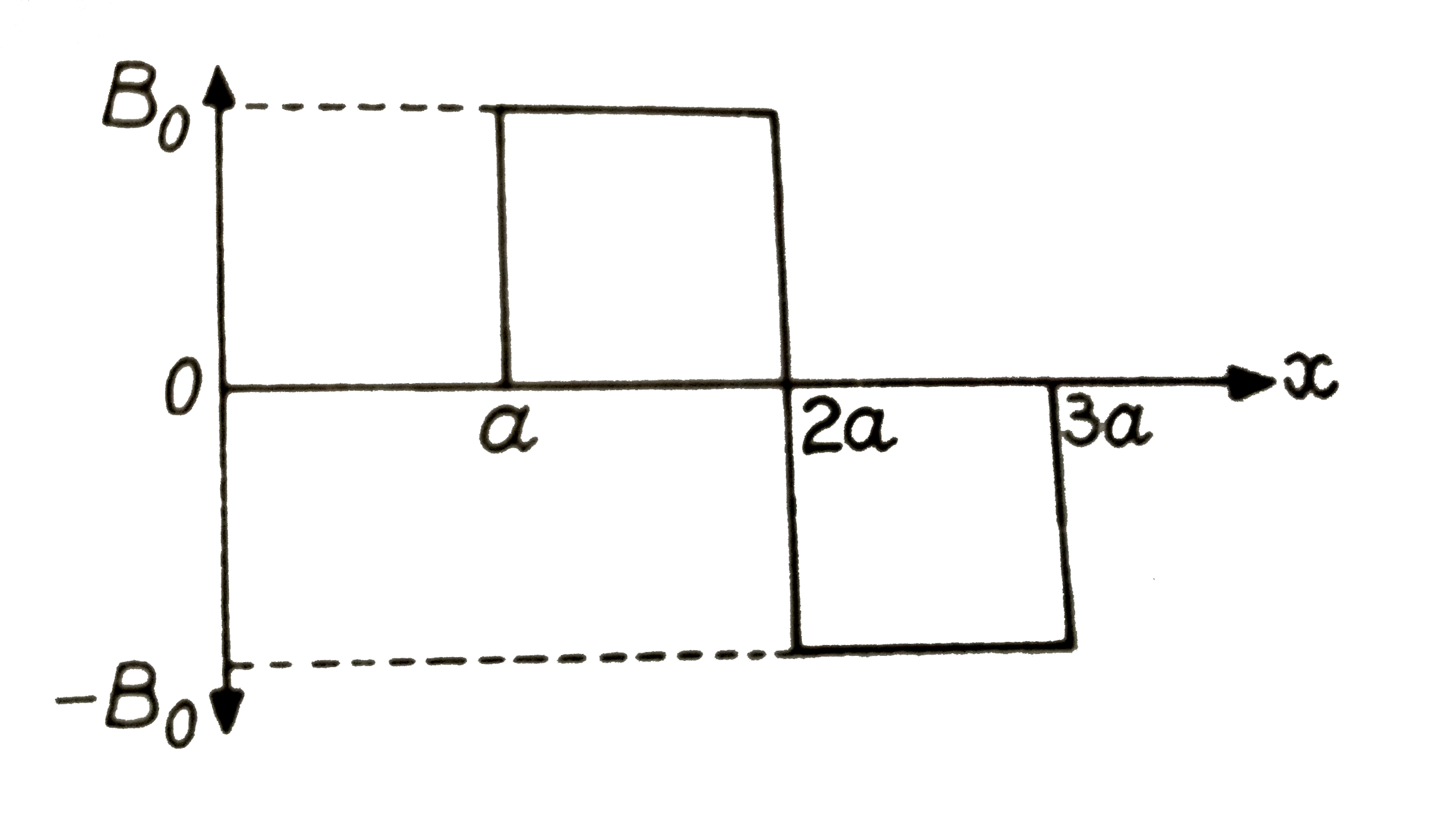
View SolutionA positive charge enters in the region of transverse magnetic field as shown in figure. Velocity of charge is in such a way that charge passes through both inward and outward magnetic field regions, then possibly correct path of the charge is
View SolutionA positive charge enters in the region of transverse magnetic field as shown in figure. Velocity of charge is in such a way that charge passes through both inward and outward magnetic field regions, then possibly correct path of the charge is
View SolutionA non-relativistic point charge q moves with a constant velocity v . Using the field transformation formula. Find the magnetic induction B produced by this charge at the point whose position relative to the charge is determind by the radius vector r .
View SolutionMagnetic induction field is existing along axis in a region is positive . A point charge is projected with a velocity at origin along positive axis , choose the correct alternative regarding its deviation.
View SolutionDetermine the trajectory of a charged particle which enters a region of magnetic field with with velocity making an angle with the field.
View SolutionA positively charged particle moving due east enters a region of uniform magnetic field directed vertically upwards. The partical will be
View SolutionA positively charged particle moving due east enters a region of uniform magnetic field directed vertically upwards. The partical will be
View Solution