Prove that the sum of the eccentric angles of the extremities of a chord which is drawn in a given direction is constant and equal to twice the eccentric angle of the point at which the tangent is parallel to the given direction.
Consider two points on the ellipse and evaluate the slope of the chord. If the slope is constant prove that the sum of the angles is constant.Slope of chord AB = mSo the slopes are equal. They are parallel to each other. Hence proved.
Related Solutions
Prove that the sum of the eccentric angles of the extremities of a chord,which is drawn in a given direction,is constant,and equal to twice the eccentric angle of the point at which the tangent is parallel to the given direction.
View SolutionThe locus of the point of intersection of tangents drawn at two points of an ellipse, whose sum of the eccentric angles is constant, is
View Solutionसिद्ध कीजिए कि यदि एक वृत्त कि स्पर्श रेखा से एक जीवा खींची जाये तो इस जीवा द्वारा दी गई स्पर्श रेखा से बनाये गये कोण क्रमशः उसी जीवा द्वारा एकान्तर वृत्तखंडो में बने कोणों के बराबर होते है।
View SolutionIf alpha and beta are the eccentric angles of the extremities of a focal chord of an ellipse, then prove that the eccentricity of the ellipse is (sinalpha+sinbeta)/("sin"(alpha+beta))
View SolutionIf are the eccentric angles of the extremities of a focal chord of an ellipse, then prove that the eccentricity of the ellipse is
View SolutionIf a chord is drawn through the point of contact of a tangent to a circle; then the angle which this chord makes with the given tangent are equal respectively to the angles formed in the corresponding alternate segments.
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionProve that tangents from extremities of any chord makes equal angle with the chord.
View SolutionA chord of a circle is equal to its radius. A tangent is drawn to the circle at an extremity of the chord. The angle between the tangent and the chord is
View SolutionProve that the tangent drawn at the ends of chord of a circle make equal angle with the chord.
View SolutionIf alphaa n dbeta are the eccentric angles of the extremities of a focal chord of an ellipse, then prove that the eccentricity of the ellipse is (sinalpha+sinbeta)/("sin"(alpha+beta))
View SolutionIf are the eccentric angles of the extremities of a focal chord of an ellipse, then prove that the eccentricity of the ellipse is
View SolutionThe locus of the point of intersection of tangents to an ellipse at two points, sum of whose eccentric angles is constant, is a/an
View SolutionThe locus of the point of intersection of tangents to an ellipse at two points sum of whose eccentric angles is constant is
View SolutionIf theta is the difference of the eccentric angles of two points on an ellipse, the tangents at which are at right angles. Prove that , where are the semi diameters parallel to the tangents at the points and a,b are the semi-axes of the ellipse.
View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
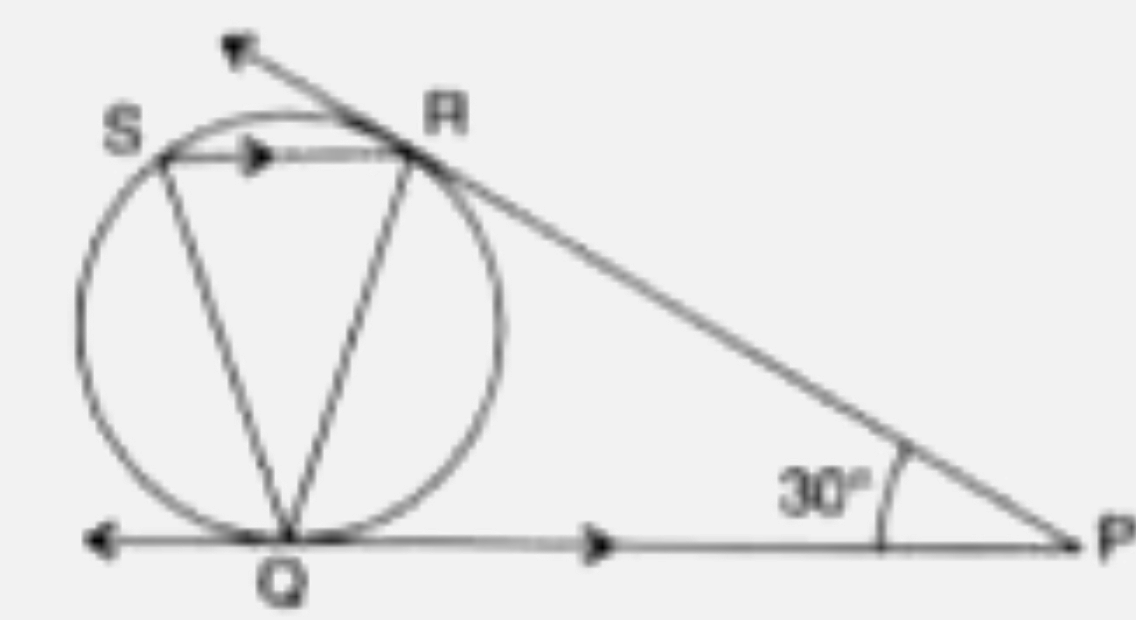
View SolutionIn the given figure, tangents PQ and PR are drawn to a circle such that angle RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the angle RQS.
View SolutionIf are the eccentric angles of the extermities of a focal chord of an ellipse, then eccentricity of the ellipse is
View Solution